
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчет колебательной составляющей статистических сумм по состоянию молекул идеального газа.
Расчет колебательной составляющей статистических сумм по состоянию молекул идеального газа.
Для каждой молекулы газа – участника химической реакции рассчитать lnQкол. Всего независимых нормальных колебаний в молекуле (n), состоящей из N атомов:
n=3N-5 для линейной молекулы n=3N-6 для нелинейной молекулы.

где gi – фактор вырождения – i-го колебания (с. 183-188 Краткого Справочника ф-х величин, в дальнейшем КС). Там же выписываете волновые числа Ваших колебаний, а именно:ν (c тильдой):
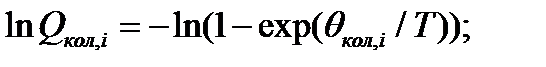
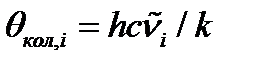
Где: h=6.6*10-34 Дж*с, с=3*108 м/с, k=1.38*10-23 Дж/К. Тогда:
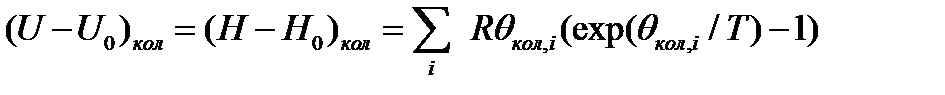
Уравнение Эйнштейна. Здесь и везде далее суммирование ведется по всем колебаниям в молекуле с учетом gi.
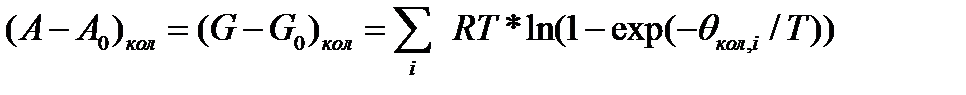
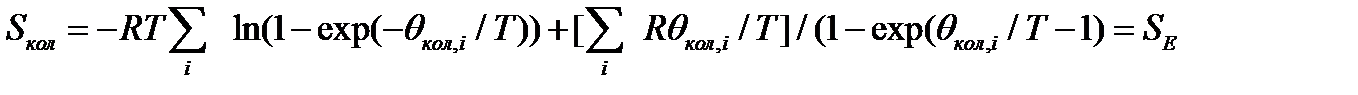
или колебательная энтропия Эйнштейна,
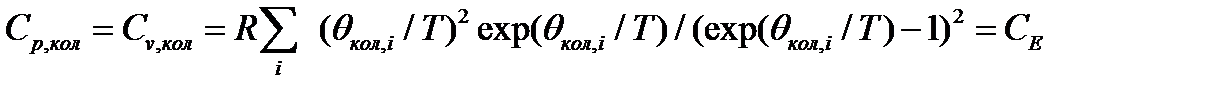
или колебательная теплоемкость Эйнштейна.
Расчет электронной составляющей статистических сумм по состоянию молекул идеального газа.
Для каждой молекулы газа – участника химической реакции рассчитать lnQэл.
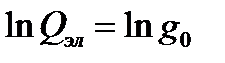
Где: g0 – фактор вырождения основного электронного состояния. Это уравнение для не слишком высоких температур – менее 3000 К.
Если в реакции принимает участие атомы, то:
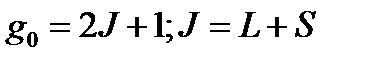
Где: L – сумма третьих - орбитальных квантовых чисел, S – сумма четвертых квантовых чисел. Заполненные электронные оболочки, подоболочки и ячейки не учитываются. Для s электронов третье квантовое число ml=0, для Р электронов ml =-1, 0 ,+1… Спин электрона составляет или -1/2, или +1/2.
Правильное заполнение электронных состояний а в атомах (а потом и в молекулах) подчиняется правилам запрета:
Принцип Паули – В атоме не может быть 2-х электронов с одинаковым набором 4-х квантовых чисел,
Первое правило Гунда (выполняется после принципа Паули) – в атоме устойчиво состояние с максимальным S,
Второе правило Гунда (выполняется после первого правила Гунда) – в атоме устойчиво состояние с максимальным L.
Например для Ar g0 = 1, для К g0 = 2*(0+1/2)+1=2, для О g0 = 2*(1+1)+1=4 и т.д.
Для подавляющего большинства молекул g0 = 1 – молекулах, как правило, нет неспаренных электронов. Если молекула – свободный радикал, то g0 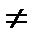 1, и его надо рассчитывать.
1, и его надо рассчитывать.
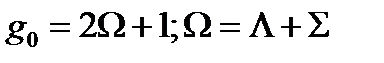
Где:  – сумма третьих - орбитальных квантовых чисел,
– сумма третьих - орбитальных квантовых чисел, 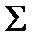 – сумма четвертых квантовых чисел. Заполненные электронные оболочки, подоболочки и ячейки не учитываются. Для
– сумма четвертых квантовых чисел. Заполненные электронные оболочки, подоболочки и ячейки не учитываются. Для  электронов ml =0, для
электронов ml =0, для 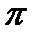 электронов ml =-1, 0 ,+1… Спин электрона опять составляет или -1/2, или +1/2.
электронов ml =-1, 0 ,+1… Спин электрона опять составляет или -1/2, или +1/2.
Например для бирадикальной молекулы O2 (она единственная может быть в Ваших примерах): g0 = 2*(0+1)+1=3, для молекулы Н2 g0 = 2*(0+0)+1=1.
Значения g0 легко также рассчитываются по термам молекул (см. КС стр.164-167).
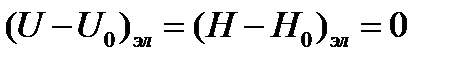

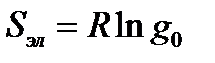
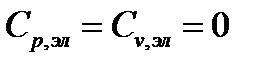
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|