
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Идентификатор конференции. Код доступа 921394. Нахождение рациональных корней многочлена
Zoom
Идентификатор конференции
976 880 4436
Код доступа 921394
Нахождение рациональных корней многочлена
Пусть дан многочлен f(x) = 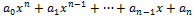 c целыми коэффициентами. Для нахождения рациональных корней многочлена можно использовать следующие факты:
c целыми коэффициентами. Для нахождения рациональных корней многочлена можно использовать следующие факты:
1. Если старший коэффициент 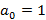 и рациональные корни существуют, то являются целыми числами, делителями свободного члена
и рациональные корни существуют, то являются целыми числами, делителями свободного члена 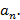
2. Если x = 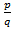 , где p и q взаимно просты, является рациональным корнем многочлена f(x), то p делит
, где p и q взаимно просты, является рациональным корнем многочлена f(x), то p делит 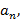 q делит
q делит 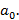
3. Если x = 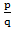 , где p и q взаимно просты, является рациональным корнем многочлена f(x), то
, где p и q взаимно просты, является рациональным корнем многочлена f(x), то 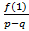 и
и 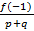 есть целые числа.
есть целые числа.
Учитывая эти утверждения, можно находить рациональные корни по следующей схеме:
1. Выписываем все делители коэффициентов 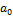 и
и 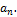
2. Вычисляем, например, по схеме Горнера значения 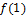 и
и 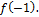
3. Находим значения 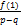 и
и 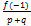 для различных взаимно простых делителей коэффициентов
для различных взаимно простых делителей коэффициентов 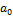 и
и 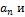 берем те значения p и q, для которых
берем те значения p и q, для которых 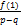 и
и 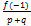 являются целыми числами.
являются целыми числами.
4. Найденные дроби 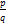 исследуем по схеме Горнера.
исследуем по схеме Горнера.
Пример. Найти рациональные корни многочлена
f(x) = 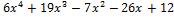 .
.
Имеем 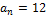 , тогда p =
, тогда p = 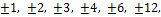
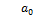 = 6, тогда q = 1, 2, 3, 6.
= 6, тогда q = 1, 2, 3, 6.
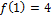 и
и 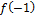 = 18, значит,
= 18, значит, 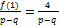 и
и 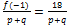 .
.
Оформим результаты исследования различных значений p и q в виде таблицы:
| q | p (p и q взаимно просты) | 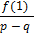
| 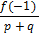
| Исследованию подлежит
x = 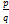
|

| 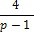
| 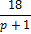
| 2; -3 | |
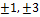
| 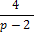
| 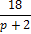
| 
| |
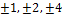
| 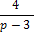
| 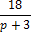
| 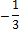
| |
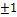
| 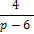
| 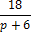
| _ |
Являются ли найденные значения х = 2; -3;  ;
; 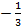 корнями многочлена, проверим по схеме Горнера:
корнями многочлена, проверим по схеме Горнера:
| -7 | -26 | вывод | ||||
| -3 | -10 | х = -3 корень | ||||

| -8 | х =  корень корень
| ||||
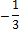
|
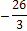
|
Можно записать разложение многочлена f(x) = (х +3) (х –  ) (6
) (6 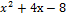 ) или f(x) = (х +3) (2х -1) (3
) или f(x) = (х +3) (2х -1) (3 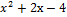 ).
).
Ответ: рациональные корни данного многочлена есть числа -3; 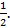
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|