
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Наибольший общий делитель многочленов
Наибольший общий делитель многочленов
Определение.Многочлен d(x) называется наибольшим общим делителем многочленов f(x) и g(x), если d(x) является делителем f(x) и g(x) и, если многочлен h(x) делит f(x) и g(x), то h(x) делит d(x). (Обозначение: d(x) = НОД(f(x), g(x))).
Наибольший общий делитель многочленов находится с точностью до постоянного множителя: если d(x) = НОД(f(x), g(x)) и с – число отличное от нуля, то сd(x) = НОД(f(x), g(x)).
Если НОД(f(x), g(x)) есть число, то многочлены f(x) и g(x) называются взаимно простыми.
Рассмотрим алгоритм Евклида, позволяющий находить наибольший общий делитель двух многочленов. Пусть deg f(x) 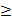 deg g(x). Разделим многочлен f(x) на многочлен g(x), получим остаток
deg g(x). Разделим многочлен f(x) на многочлен g(x), получим остаток 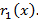 Затем g(x) разделим на
Затем g(x) разделим на 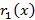 , получим остаток
, получим остаток 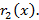 Затем каждый многочлен
Затем каждый многочлен 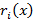 делим на
делим на  , обозначая остаток через
, обозначая остаток через  . Так как степени остатков убывают, то на некотором шаге остаток будет равен нулю. Таким образом, имеем:
. Так как степени остатков убывают, то на некотором шаге остаток будет равен нулю. Таким образом, имеем:
f(x) = g(x) 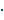
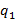 (x) +
(x) + 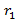 (x), deg
(x), deg 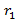 (x)
(x)  deg g(x);
deg g(x);
g(x)= 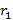 (x)
(x) 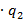 (x)+
(x)+ 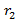 (x), deg
(x), deg 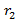 (x)
(x)  deg
deg 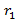 (x);
(x); 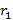 (x)=
(x)= 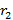 (x)
(x)  (x)+
(x)+  (x), deg
(x), deg  (x)
(x)  deg
deg 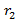 (x); …………………………………………………………….
(x); ……………………………………………………………. 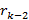 (x) =
(x) = 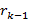 (x)
(x) 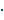
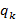 (x) +
(x) + 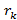 (x), deg
(x), deg 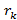 (x)
(x)  deg
deg 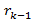 (x);
(x); 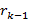 (x) =
(x) = 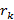 (x)
(x) 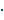
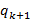 (x).
(x).
Утверждение.Последний отличный от нуля остаток 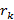 (x) в алгоритме Евклида является наибольшим общим делителем многочленов f(x) и g(x).
(x) в алгоритме Евклида является наибольшим общим делителем многочленов f(x) и g(x).
Пример.Найти наибольший общий делитель многочленов f(x)= 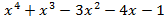 и g(x)=
и g(x)= 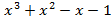 .
.
Применим алгоритм Евклида:
_ 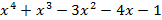 |
| 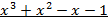
 |
| 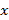
 2
2 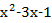
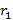 (x)=
(x)= 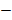 2
2 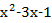 ;
;
_ 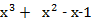 |
| 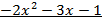
 |
|  + 0,25
+ 0,25 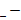 0,5
0,5 
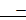 0,5
0,5 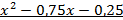

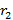 (x)=
(x)=  ;
;
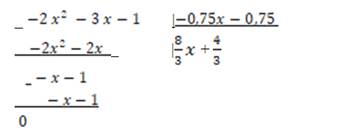
 (x)= 0. Значит НОД(f(x), g(x))=
(x)= 0. Значит НОД(f(x), g(x))=  .
.
Так как наибольший общий делитель определяется с точностью до постоянного множителя, то удобно считать что НОД(f(x), g(x))= 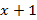 .
.
Утверждение.Если d(x) наибольший общий делитель многочленов f(x) и g(x), то найдутся такие многочлены u(x) и v(x), что d(x) = u(x) f(x) + v(x) g(x), где степень u(x) меньше степени g(x), а степень v(x) меньше степени f(x).
Утверждение.Многочлены f(x) и g(x) тогда и только тогда взаимно просты, когда можно найти многочлены u(x) и v(x), удовлетворяющие равенству
u(x) f(x) + v(x) g(x) = 1, где deg f(x) 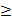 deg v(x) и deg g(x)
deg v(x) и deg g(x) 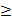 deg u(x).
deg u(x).
Пример.Применяя алгоритм Евклида, найти такие многочлены u(x) и v(x), чтобы НОД(f(x), g(x)) = u(x) f(x) + v(x) g(x), где
f(x)= 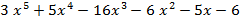 , g(x)=
, g(x)= 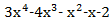 .
.
_ 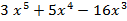
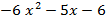 |
| 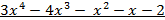
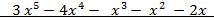 |
| 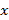 + 3
+ 3 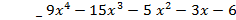
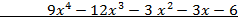
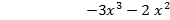
f(x) = g(x)(  + 3) +
+ 3) +  .
.

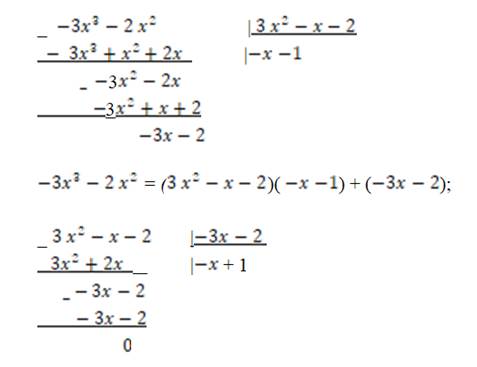
 = (
= ( 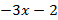 )(
)( 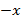 + 1).
+ 1).
Таким образом, НОД(f(x), g(x)) =  .
.
Далее, двигаясь по алгоритму Евклида снизу вверх, имеем:
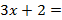 (
(  )(
)( 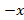
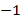 ) + (
) + ( 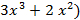 ,
,
 = g(x)+
= g(x)+  )(
)( 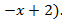 Следовательно,
Следовательно,
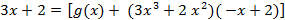 (
( 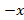
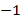 ) + (
) + ( 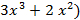 .
.
Поскольку 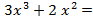 g(x)(
g(x)(  + 3)
+ 3) 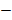 f(x), получаем
f(x), получаем
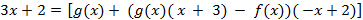 (
( 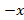
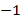 ) + g(x)(
) + g(x)(  + 3)
+ 3) 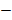 f(x), или
f(x), или
 = f(x)
= f(x) 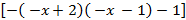 + g(x)
+ g(x) 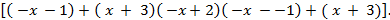 Окончательно имеем:
Окончательно имеем:
 = f(x)(
= f(x)( 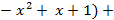 g(x)(
g(x)( 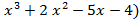 , т.е.
, т.е.
u(x)= ( 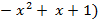 , v(x)= (
, v(x)= ( 
Пример.Не применяя алгоритм Евклида, найти такие многочлены u(x) и v(x), чтобы
u(x) f(x) + v(x) g(x) = 1, где f(x) = 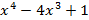 , g(x)=
, g(x)= 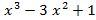 .
.
Учитывая, что deg f(x) 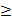 deg v(x) и deg g(x)
deg v(x) и deg g(x) 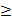 deg u(x), имеем:
deg u(x), имеем:
f(x)( 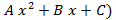 + g(x)(
+ g(x)(  или
или
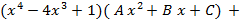 (
( 
Для нахождения неопределенных коэффициентов А,В,С.К,  приравниваем коэффициенты при одинаковых степенях
приравниваем коэффициенты при одинаковых степенях 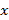 в левой и правой частях этого равенства. Имеем систему:
в левой и правой частях этого равенства. Имеем систему: 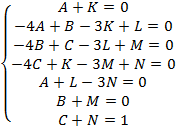 , откуда находим А=
, откуда находим А= 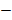 К =
К = 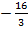 , В=
, В= 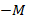 =
= 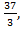 С=
С= 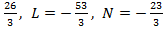 . Окончательно получаем u(x)=
. Окончательно получаем u(x)= 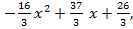 v(x)=
v(x)= 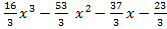 .
.
Работа 5. Применяя алгоритм Евклида, найти наибольший общий делитель многочленов f(x) и g(x)
- f(x)=
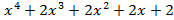 , g(x)=
, g(x)= 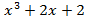
- f(x)=
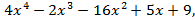 g(x)=
g(x)= 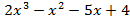
- f(x)=
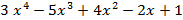 , g(x)=
, g(x)= 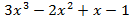
- f(x) =
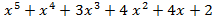 , g(x)=
, g(x)= 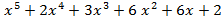
- f(x) =
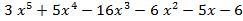 , g(x)=
, g(x)= 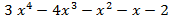
- f(x) =
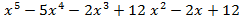 , g(x)=
, g(x)= 
- f(x)=
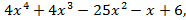 g(x)=
g(x)= 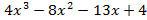
- f(x)=
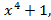 g(x)=
g(x)= 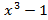
- f(x)=
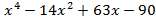 , g(x)=
, g(x)= 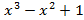
- f(x)=
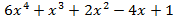 , g(x)=
, g(x)= 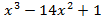
Практика
Zoom
Идентификатор конференции
976 880 4436
Безопасность
Код доступа 921394
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|