
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа по теме: «Первообразная и интеграл»
Контрольная работа по теме: «Первообразная и интеграл»
Вариант №1.
| № п/п | Задание | Способ выполнения |
Укажите функцию, для которой F(x) = 4sinx – x является первообразной.
a) y = 4sinx – 1;
b) y = 4cosx – 1;
c) y = 4sinx – 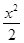 ;
d) y = 4cosx – ;
d) y = 4cosx – 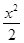 . .
| Выберите правильный ответ из предложенных вариантов и за-пишите его. | |
| График первообразной для функции y = 6x2 – 7x + 5 проходит через точку О (0;0). Найдите эту первообразную. | Решите задачу, запишите решение и ответ | |
Укажите на каком рисунке изображен график первообразной для функции у = -4х .
1)  2) 2) 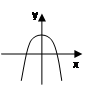 3)
3) 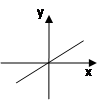
| Выберите правильный ответ из предложенных вариантов и за-пишите его. | |
| Завершите предложение так, чтобы получилось истинное высказывание: «Площадь криволинейной трапеции, ограниченной сверху графиком непрерывной и неотрицательной на [a;b] функции y = f(x) и прямыми x = a, x = b (a<b), y=0 вычисляется как…» a) сумма значений функции y = f(x) в точках a и b; b) разность значений производной функции y = f(x) в точках a и b; c) сумма значений первообразной для функции y = f(x) в точках a и b; d) разность значений первообразной для функции y = f(x) в точках a и b. | Выберите правильный ответ из предложенных вариантов и за-пишите его. | |
| Вычислите площадь фигуры, ограниченной линиями y = 4х – х2 и y = 0. | Выполните задание, запишите решение и ответ | |
Вычислите 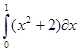
| Выполните задание, запишите решение и ответ |
Вариант №2.
| № п/п | Задание | Способ выполнения |
Укажите функцию, для которой F(x) = 19sinx + x2 является первообразной.
a) y = 19sinx + 2x;
b) y = 19cosx + 2x;
c) y = 19sinx + x3;
d) y = -19cosx + 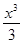 ; ;
| Выберите правильный ответ из предложенных вариантов и за-пишите его. | |
| График первообразной для функции y = 3x3 + 12x - 5 проходит через точку О(0;0). Найдите эту первообразную. | Решите задачу, запишите реше-ние и ответ | |
Укажите на каком рисунке изображен график первообразной для функции у = 3х2 .
1) 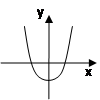 2) 2) 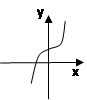 3) 3) 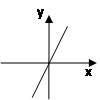
| Выберите правильный ответ из предложенных вариантов и за-пишите его. | |
Завершите предложение так, чтобы получилось истинное высказывание:
« Вычислить интеграл 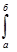 f(x)dx – значит, найти…»
a) сумма значений функции y = f(x) в точках a и b;
b) разность значений производной функции y = f(x) в точках a и b;
c) сумма значений первообразной для функции y = f(x) в точках a и b;
d) разность значений первообразной для функции y = f(x) в точках a и b; f(x)dx – значит, найти…»
a) сумма значений функции y = f(x) в точках a и b;
b) разность значений производной функции y = f(x) в точках a и b;
c) сумма значений первообразной для функции y = f(x) в точках a и b;
d) разность значений первообразной для функции y = f(x) в точках a и b;
| Выберите правильный ответ из предложенных вариантов и за-пишите его. | |
| Вычислите площадь фигуры, ограниченной линиями y = 5x – x2 и y = 0. | Выполните задание, запишите решение и ответ | |
Вычислите 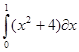
| Выполните задание, запишите решение и ответ |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|