Тема урока «Решение систем неравенств с одной переменной»

10.04.2020 Тема урока «Решение систем неравенств с одной переменной»

Продолжаем изучение темы «Решение систем неравенств с одной переменной»

Повторите § 35 (стр. 194-197).

Вспомним алгоритм решения систем неравенств с одной переменной:

1. Решить каждое из неравенств системы.

2. Изобразить множество решений каждого неравенства на координатной прямой.

3. Найти пересечение промежутков (если оно есть) и записать в виде обозначения промежутка или в виде неравенства, задающего этот промежуток, или сделать вывод об отсутствии решения системы.

Рассмотрите примеры решения систем неравенств с одной переменной и примеры решения текстовых задач при помощи систем неравенств с одной переменной по следующим материалам:

Видеоурок по ссылке https://www.youtube.com/watch?v=kLCQCUBiZbw

Пример 1. Рассмотрим решение текстовой задачи систем неравенств с одной переменной:

Задача. Турист вышел с турбазы по направлению к станции, расположенной на расстоянии 20 км. Если турист увеличит скорость на 1 км/ч, то за 4 ч он пройдёт расстояние, большее 20 км. Если он уменьшит скорость на 1 км/ч, то даже за 5 ч не успеет дойти до станции. Какова скорость туриста?

Решение: Пусть скорость туриста равна х км/ч. Если турист будет идти со скоростью (х + 1) км/ч, то за 4 ч он пройдёт 4(х + 1) км. По условию задачи 4(x + 1) > 20. Если турист будет идти со скоростью (x - 1) км/ч, то за 5 ч он пройдёт 5(х - 1) км. По условию задачи 5(x- 1) < 20.

Требуется найти те значения х, при которых верно как неравенство 4(x + 1) > 20, так и неравенство 5(x - 1) < 20, т. е. найти общие решения этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют запись

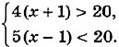
Заменив каждое неравенство системы равносильным ему неравенством, получим систему

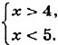
Значит, значение х должно удовлетворять условию 4 < х < 5. Ответ: скорость туриста больше 4 км/ч, но меньше 5 км/ч.

12 Следующая ⇒