- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Параллелепипед
Прямоугольный паралелепипед
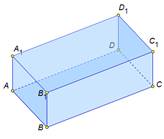
| Для изучения сегодняшней темы поговорим о незаменимом помощнике каждого школьника –ластике. | На экране изображение:
| ||
| Что можно сказать о форме ластиков? Что бы анализировать форму предметов было удобно, перенесем их на чертёж. Итак, первый ластик изобразим в форме фигуры в основании которой лежит прямоугольник, такой же прямоугольник и в верхней параллельной плоскости. Боковые грани прямоугольники, причём противоположные грани, равные прямоугольники. Получилась вот такая фигура. И нам она знакома –это параллелепипед. У второго ластика лишь одно отличие. Две боковых грани ластика параллелограммы. И это тоже параллелепипед. В чём же тогда фокус? Дело в том, что оба ластика действительно демонстрируют геометрическую фигуру параллелепипед, но разные его виды. Давайте разберемся в подробностях. Параллелепипед, ребра которого перпендикулярны к плоскости основания, называется прямым параллелепипедом. У такого параллелепипеда все грани прямоугольники. Параллелепипед, ребра которого наклонены к плоскости основания, под острым углом, называется наклонным параллелепипедом. А прямой параллелепипед в основании которого лежит прямоугольник, называется прямоугольным параллелепипедом. На этом виде параллелепипеда мы и остановимся по подробней, так как это самая распространяя форма окружающих нас предметов. Посмотрите сами. Книги, блок от компьютера, микроволновая печь и многое другое. |
На экране изображение:
На экране таблица |
Параллелепипед

Прямой
(ребра перпендикулярны основаниям)
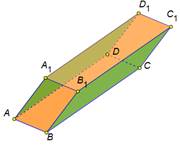
| Наклонный
(ребра наклонены к плоскости основания под углом) 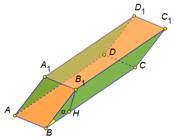
|
Прямоугольный
(прямой параллелепипед в основании которого лежит прямоугольник)
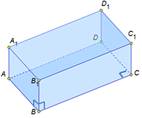
|
На экране изображение:



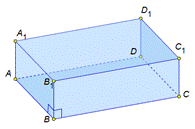
 На экране под изображением текст:
Свойство 2. Все двухгранные углы прямоугольного параллелепипеда –прямые
На экране под изображением текст:
Свойство 2. Все двухгранные углы прямоугольного параллелепипеда –прямые
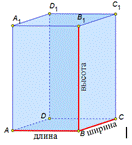
| Длины трёх рёбер, имеющих общую вершину называются измерениями прямоугольного параллелепипеда. |
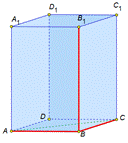
| Квадрат диагонали прямоугольника АВСD равен сумме квадратов двух его измерений.
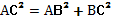
|
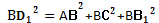 .
Мы уже сказали, что диагональ АС прямоугольника АВСD равна сумме квадратов ребер АВ и ВС, но диагонали прямоугольника равны, значит квадрат диагонали DB равен сумме квадратов ребер АВ и ВС.
Ребро ВВ1 по определению прямоугольного параллелепипеда перпендикулярно плоскости основания, значит перпендикулярно диагонали основания DB и треугольник прямоугольный. Значит, для треугольника справедлива теорема Пифагора. Квадрат диагонали
.
Мы уже сказали, что диагональ АС прямоугольника АВСD равна сумме квадратов ребер АВ и ВС, но диагонали прямоугольника равны, значит квадрат диагонали DB равен сумме квадратов ребер АВ и ВС.
Ребро ВВ1 по определению прямоугольного параллелепипеда перпендикулярно плоскости основания, значит перпендикулярно диагонали основания DB и треугольник прямоугольный. Значит, для треугольника справедлива теорема Пифагора. Квадрат диагонали 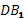 равен сумме квадратов катетов DB и
равен сумме квадратов катетов DB и 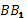 .
Подставим в равенство значение диагонали DB и получим выражение.
Что и требовалось доказать.
Прямоугольники DD1B1B и АА1С1С равны, так как равны их стороны. Значит диагонали этих прямоугольников также равны, но они являются диагоналями прямоугольного параллелепипеда, следовательно справедливо утверждение – диагонали прямоугольного параллелепипеда равны. Это утверждение можно считать следствием доказанного свойства.
.
Подставим в равенство значение диагонали DB и получим выражение.
Что и требовалось доказать.
Прямоугольники DD1B1B и АА1С1С равны, так как равны их стороны. Значит диагонали этих прямоугольников также равны, но они являются диагоналями прямоугольного параллелепипеда, следовательно справедливо утверждение – диагонали прямоугольного параллелепипеда равны. Это утверждение можно считать следствием доказанного свойства.
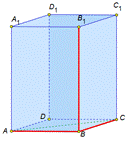
| Дано: АВСВA1B1C1D1- прямоуг. паралле-д.
Доказать: 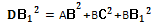
|
На экране добавляется пункт 1)
1) DB2= АС2= 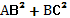 (по свойству прямоугольника)
(по свойству прямоугольника)
На экране добавляется пункт 2)

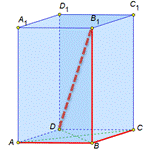
| 2) ВВ1 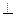 DB
DB12=DB2+BB12. DB
DB12=DB2+BB12.
|
На экране добавляется пункт 3) с анимацией последнего выражения.
| 3) 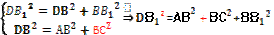
|
На экране текст и изображение:
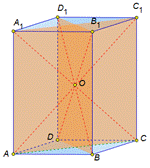
| Диагонали прямоугольного параллелепипеда равны. |
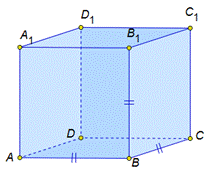
| Это прямоугольный параллелепипед, у которого все три измерения равны (все ребра равные). |
 будет равен выражению.
По теореме Пифагора из прямоугольного треугольника А1АВ справедливо равенство
По теореме Пифагора из прямоугольного треугольника С1СВ справедливо равенство
По свойству прямоугольника АВСD справедливо равенство
будет равен выражению.
По теореме Пифагора из прямоугольного треугольника А1АВ справедливо равенство
По теореме Пифагора из прямоугольного треугольника С1СВ справедливо равенство
По свойству прямоугольника АВСD справедливо равенство  Составим систему из полученных равенств. Почленно сложим эти равенства. Получили удвоенную сумму квадратов трех измерений параллелепипеда.
А это есть диагональ
Составим систему из полученных равенств. Почленно сложим эти равенства. Получили удвоенную сумму квадратов трех измерений параллелепипеда.
А это есть диагональ 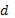 . После преобразований выражения получили, что диагональ равна 21 см.
. После преобразований выражения получили, что диагональ равна 21 см.
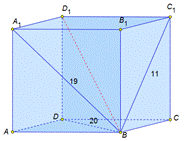
| Дано: АВСВA1B1C1D1–пр. пар-д ВС1 = 11 см, А1В = 19 см, DВ = 20 см. Найти: D1В |
На экране выражение:
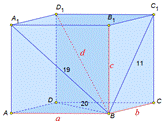
| Решение:
1) 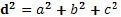 (по свойству прям. паралле-да) (по свойству прям. паралле-да)
|
На экране пункт 2)
2)А1А 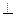 AB
AB 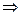 Δ А1АВ-прям-й
Δ А1АВ-прям-й 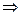 A1B2=a2+c2
A1B2=a2+c2
На экране пункт 3)
3)С1С 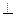 BC
BC 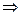 ΔС1СВ-прям-й
ΔС1СВ-прям-й 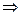 C1B2=b2+c2
C1B2=b2+c2
На экране пункт 4)
4)ABCD–прямоугольник  DB2=a2+b2
DB2=a2+b2
На экране пункт 5) с анимацией выхода элементов текста
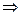
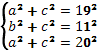
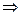 2(a2+b2+c2)=192+112+202
2(a2+b2+c2)=192+112+202 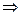
2 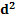 =
= 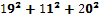 ⟹
⟹ 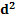 =
= 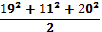 =441⟹
=441⟹ 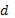 =21 см.
=21 см.
Ответ: 21 см.
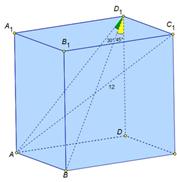
| Решение:
1) AB 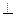 ( АА1D1D) ( АА1D1D) 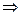 АD1– проекция ВD1 АD1– проекция ВD1 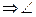 AD1В=30° AD1В=30°
|
На экране пункт 2)
2) ВD1=АС1=12 см (по свойству)
На экране добавляется пункт 3) и выносным чертежом:
3) △D1AB-прям-й, 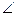 A D1B=30°, D1B=12 см , A D1B=30°, D1B=12 см , 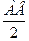 =6 см. =6 см.
|
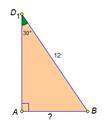
|
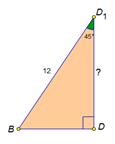
На экране пункт 4) с выносным чертежом:
4) △ BDD1– прям-й, ∠ BDD1=45°⟹
BD=DD1=12cos45°=12· 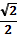 =6 =6 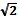 см. см.
| 
|
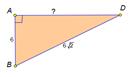
На экране пункт 5) и выносной чертёж:
5) △ BAD– прямоугольный, АВ=6 см, BD=6 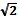 см
AD= см
AD= 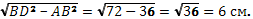
| 
|
На экране текст:
Ответ: 6см, 6см, 6 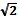 см.
см.