
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение неравенств с одной переменной
Решение неравенств с одной переменной
Вспоминаем последние уроки четверти, открываем классную работу с объяснением материала.
1. Правила решения неравенств
1. Неравенство 5х – 11 > 3 содержит переменную х. При подстановке некоторых числовых значений вместо х мы можем получить как верное, так и неверное числовое неравенство. Н а п р и м е р:
при х = 4 неравенство 5 · 4 – 11 > 3 – верное (9 > 3), а
при х = 2 неравенство 5 · 2 – 11 > 3 – неверное (–1 > 3). Говорят, что число 4 является решением неравенства или удовлетворяет неравенству.
О п р е д е л е н и е 1: Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
О п р е д е л е н и е 2: Решить неравенство – значит найти все его решения или доказать, что решений нет.
2. Чтобы решать неравенства, необходимо уметь их преобразовывать к неравенству вида ах > b или ax < b (где a и b – некоторые числа). Неравенства такого вида называют линейными неравенствами с одной переменной. Данное неравенство должно быть равносильно исходному.
О п р е д е л е н и е 3: Неравенства, имеющие одни и те же решения, называются равносильными.
3. По учебнику на с. 177 разобрать основные свойства, используемые при преобразовании неравенства с одной переменной к равносильному неравенству.
4. Разобрать примеры 1, 2 по учебнику со с. 177–178.
2. Выполнение упражнений
1) №835 Образец
а) х + 8 > 0;
х > –8;
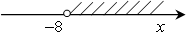
Ответ: хϵ(-8;+∞)
Не забываем, про три способа записать ответ!!!
б) х – 7 < 0;
1 способ: х < 7;
2 способ: 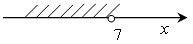
3 способ: хϵ(-∞;7)
Все три способа используются при записи ответов на экзамене.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|