Тема 1.2. Плоская система сходящихся сил.

ЛЕКЦИЯ 3

Тема 1.2. Плоская система сходящихся сил.

Определение равнодействующей

аналитическим способом

Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в аналитической форме.

Уметь определять проекции силы на две взаимно перпендикулярные оси, решать задачи на равновесие в аналитической форме.

Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).

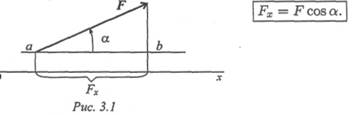
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

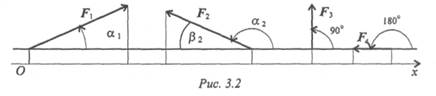
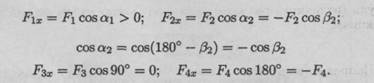
Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).

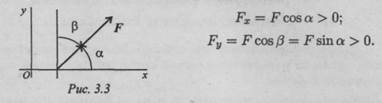
Определение равнодействующей системы сил аналитическим

способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси х и у (рис. 3.46).

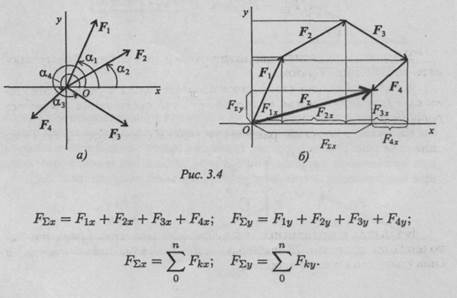
Модуль (величину) равнодействующей можно найти по известным проекциям:

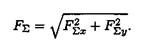
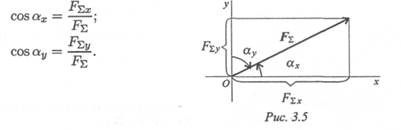
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).

12 3 Следующая ⇒