- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема «Параллельные прямые в пространстве. Признак параллельности прямых. Решение задач».
Тема «Параллельные прямые в пространстве. Признак параллельности прямых. Решение задач».
1.Параллельность прямых.
Определение: Две прямые в пространстве называются параллельными, если они не пересекаются.
Определение: Две прямые в пространстве называются скрещивающимися, если они не пересекаются и не лежат в одной плоскости.
Взаимное расположение прямых в пространстве.
| Пересекающиеся прямые | Скрещивающиеся прямые | Параллельные прямые | |||||||||||||||||||||||||||||

| 

| 

| |||||||||||||||||||||||||||||
 Теорема 1.4 Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.
Теорема 1.4 Через точку вне данной прямой можно провести прямую, параллельную данной, и притом только одну.
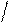
 Дано: точка А
Дано: точка А 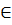 а
а
Доказать: 1)Что через т.А можно провести
2) Что единственная
Признак параллельности прямых.
Теорема 1.5 Две прямые, параллельные третьей прямой, параллельны.
Рассматриваем два случая.
| Все прямые принадлежат одной плоскости | Прямые принадлежат разным плоскостям |
   
|    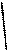    
|
Вопросы для самоконтроля.
1. Какие прямые называются параллельными?
2. Какие прямые называются скрещивающимися?
3. Назовите признак параллельности прямых в пространстве.
Изобразите в тетради:
1. Две параллельные прямые в плоскости 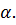
2. Три параллельные прямые не лежащие в одной плоскости.
Решите задачу:
Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках 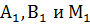 . Найдите длину отрезка М
. Найдите длину отрезка М 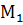 , если отрезок АВ не пересекает плоскость и если:
, если отрезок АВ не пересекает плоскость и если:
1) 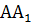 = 5м,
= 5м, 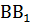 = 7м; 2)
= 7м; 2) 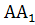 = 3,6 дм,
= 3,6 дм, 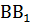 = 4,8 дм;
= 4,8 дм;
Пример
1) 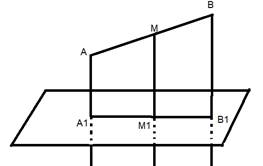
| Дано: АВ – отрезок, α – плоскость, М – точка, АМ=МВ. АА1 II ММ1 II ВВ1, АА1∩α=А1, ВВ1∩α=В1, ММ1∩α=М1, АА1=5 м., ВВ1=7 м. Найти:ММ1 |
| Решение: точки А1, В1 и М1 лежат на прямой А1В1, прямой пересечения плоскостей α и β. По теореме Фалеса М1 середина отрезка А1В1, значит ММ1 — средняя линия трапеции АА1В1В и по теореме о средней линии:
Ответ ММ1=6 метров. | |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|







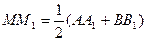 , следовательно
, следовательно