
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 21. Краткие теоретические сведения
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 21
Тема:Нахождение длин векторов и компланарных векторов в параллелепипеде.Нахождение координат векторов в пространстве
Цель:выработать практические навыкивыполнения действий с векторами в пространстве
Краткие теоретические сведения
Вектором называется направленный отрезок прямой.
Вектор с началом в точке А и концом в точке В обозначается 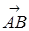 . Для обозначения векторов употребляются также строчные латинские буквы:
. Для обозначения векторов употребляются также строчные латинские буквы: 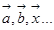 .
.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы, направленные в одну сторону, называются сонаправленными. Коллинеарные векторы, направленные в противоположные стороны, - противоположнонаправленными.
Два вектора называются равными, если они сонаправлены и равны по модулю.
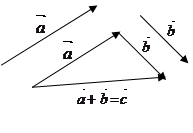 Сложениевекторов. Для того чтобы построить сумму трех и более векторов
Сложениевекторов. Для того чтобы построить сумму трех и более векторов 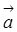 ,
, 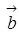 ,
, 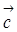 и т. д. нужно выбрать произвольную точку А и отложить от неё вектор
и т. д. нужно выбрать произвольную точку А и отложить от неё вектор 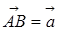 , а затем от точки В отложить вектор
, а затем от точки В отложить вектор 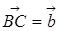 , от точки С отложите вектор СD =
, от точки С отложите вектор СD = 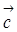 и т.д. Тогда вектор, началом которого является точка А, а концом крайняя точка последнего в сумме вектора является искомой суммой данных векторов.
и т.д. Тогда вектор, началом которого является точка А, а концом крайняя точка последнего в сумме вектора является искомой суммой данных векторов.
Координаты вектора 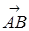 с началом в точке А(х1;y1;z1) и концом в точке В (х2;y2;z2) равны (x2 – x1; y2 – y1; z2 – z1).
с началом в точке А(х1;y1;z1) и концом в точке В (х2;y2;z2) равны (x2 – x1; y2 – y1; z2 – z1).
Длина вектора 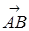 вычисляется по формуле:
вычисляется по формуле:
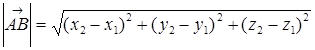 .
.
Суммой векторов 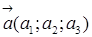 и
и 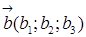 называется вектор
называется вектор 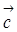 с координатами
с координатами 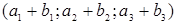 .
.
Произведением вектора 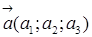 на число
на число 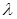 называется вектор
называется вектор 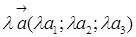 .
.
Содержание работы
I вариант
Изобразите параллелепипед ABCDA1B1C1D1 в декартовой системе координат, причем, точка B (0;0;0), AB=3; BC=4; BB1=5
- Найдите вектор, равный сумме векторов АВ, А1D1 и СА1.
- Найдите вектор, равный
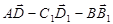 .
. - Представьте вектор ВС1 в виде разности двух векторов, один из которых вектор ВD1.
- Упростите выражение:
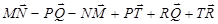 .
. - Упростите выражение:
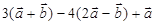 .
. - Найти координаты векторов: BA, BD, BD1, A1D
II вариант
Изобразите параллелепипед ABCDA1B1C1D1 в декартовой системе координат, причем, точка A (0;0;0), AB=5; BC=3; BB1=4
- Найдите вектор, равный сумме векторов СА1, АD и D1C1.
- Найдите вектор, равный
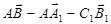 .
. - Представьте вектор ВС1 в виде разности двух векторов, один из которых вектор D1B.
- Упростите выражение:
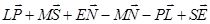 .
. - Упростите выражение:
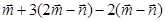 .
. - Найти координаты векторов: BA, BD, BD1, A1D
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|