Пример.. Определение.. Определение.

Пример.

Определение.

Числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией D.

Определение.

Средним квадратическим отклонениемназывают:

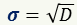
Чем меньше эти значения, тем плотнее группируются данные измерения вокруг среднего значения.

Существует алгоритм вычисления дисперсии данных.

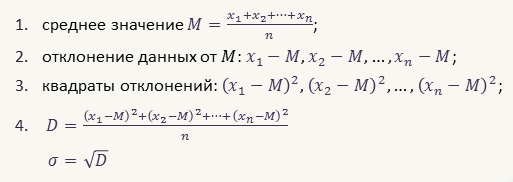
Воспользуемся этим алгоритмом и найдём значение дисперсии результатов отклонения для каждого ружья.

Проведём подсчёты для ружья А. Их удобно производить в таблице.

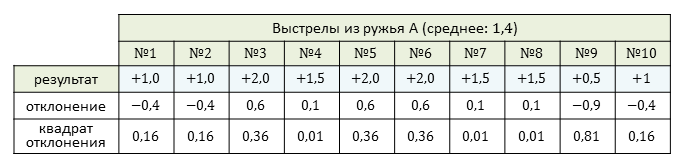
Найдём их среднее значение. Получаем, что дисперсия равна:

А среднее квадратическое отклонение равно:

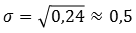
Вычислим значение дисперсии для ружья Б.

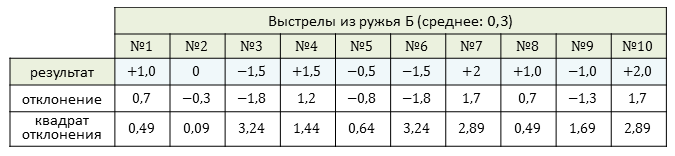
Можем вычислить дисперсию как среднее квадратов отклонений.

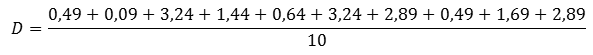
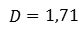
Тогда среднее квадратическое отклонение равно:

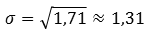
Видим, что дисперсии отличаются практически в 7 раз, а средние квадратические отклонения примерно в 3 раза.

Можно сказать, что ружьё Б стреляет с разбросом в 3 раза большим, чем ружьё А. Поэтому ружьё А точнее.

Подведём итоги нашего урока.

Сегодня вы познакомились и рассмотрели на примерах этапы статистической обработки данных.

Каждое значение, полученное в ходе измерений, мы договорились называть вариантой. А число повторений данной варианты, называют её кратностью.

Вы познакомились с формулой отыскания частоты варианты. И научились составлять таблицу распределения частот.

Также узнали, что числовую характеристику данных измерения, отвечающую за разброс данных вокруг среднего значения, называют дисперсией.