
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Многочлен Ньютона
Многочлен Ньютона
Другая форма записи интерполяционного многочлена – интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция 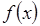 задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном порядке.
задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном порядке.
Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:
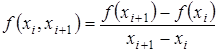 (3.14)
(3.14)
Разделенные разности второго порядка определяются через разделенные разности первого порядка:
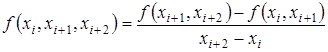 (3.15)
(3.15)
Разделенные разности k-го порядка определяются через разделенные разности порядка 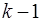 :
:
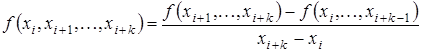 (3.16)
(3.16)
Используя понятие разделенной разности интерполяционный многочлен Ньютона можно записать в следующем виде:

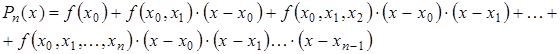 (3.17)
(3.17)
За точностью расчета можно следить по убыванию членов суммы (3.17). Если функция достаточно гладкая, то справедливо приближенное равенство 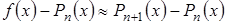 . Это приближенное равенство можно использовать для практической оценки погрешности интерполяции:
. Это приближенное равенство можно использовать для практической оценки погрешности интерполяции: 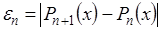 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|