
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формулы приведения
Формулы приведения
Используем формулы сложения для упрощения выражений:
1)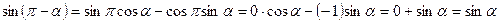
2)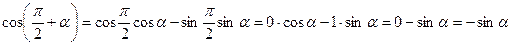
Существуют формулы, которые дают более быстрый способ упрощения таких выражений, называются они формулы приведения.
Формулы приведения – это формулы сложения, но только для углов 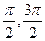 ,
, 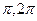 . Их 32 формулы:
. Их 32 формулы: 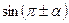 ,
,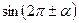 ,
, 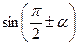 ,
, 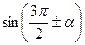 ,
,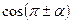 ,
,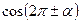 ,
, 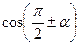 ,
, 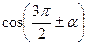 ,
,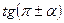 ,
,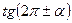 ,
, 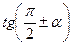 ,
, 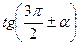 ,
, 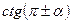 ,
,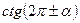 ,
, 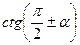 ,
, 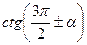 , где
, где 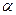 - угол I четверти!!!
- угол I четверти!!!
Запоминать 32 формулы необязательно. Есть правила для записи любой из них.
1) Если в скобке углы 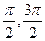 , тоназвание функций изменяется: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
, тоназвание функций изменяется: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
2) Если в скобке углы 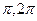 , тоназвание функций не изменяется.
, тоназвание функций не изменяется.
3) Определяется четверть угла любой из скобок 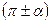 ,
, 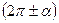 ,
, 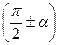 ,
, 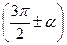 .
.
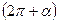 , , 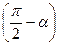 - I четверть - I четверть
| 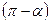 , , 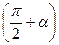 - II четверть - II четверть
|
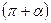 , , 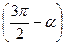 - III четверть - III четверть
| 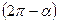 , , 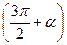 - IV четверть - IV четверть
|
4) В правой части формулы ставится тот знак, который имеет тригонометрическая функция в левой части формулы.
Пример 1:
Покажем, как с помощью этих правил можно получить формулы приведения.
1) 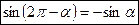 (в скобке угол
(в скобке угол 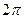 , название функции не изменяется, остается синус, скобка определяет угол IV четверти, синус в этой четверти имеет знак «-»).
, название функции не изменяется, остается синус, скобка определяет угол IV четверти, синус в этой четверти имеет знак «-»).
2) 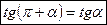 (в скобке угол
(в скобке угол 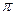 , название функции не изменяется, остается тангенс, скобка определяет угол III четверти, тангенс в этой четверти имеет знак «+»).
, название функции не изменяется, остается тангенс, скобка определяет угол III четверти, тангенс в этой четверти имеет знак «+»).
3) 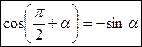 (в скобке угол
(в скобке угол 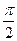 , название функции изменяется на синус, скобка определяет угол II четверти, косинус в этой четверти имеет знак «-»).
, название функции изменяется на синус, скобка определяет угол II четверти, косинус в этой четверти имеет знак «-»).
4) 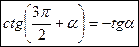 (в скобке угол
(в скобке угол 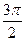 , название функции изменяется на тангенс, скобка определяет угол IV четверти, котангенс в этой четверти имеет знак «-»).
, название функции изменяется на тангенс, скобка определяет угол IV четверти, котангенс в этой четверти имеет знак «-»).
Примечание: 1)знак в правой части формулы определяется по тригонометрической функции в левой части формулы.
2) в скобке на первом месте должны стоять 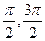 ,
, 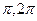 .
.
5) 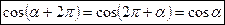 (в скобке угол
(в скобке угол 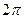 не на первом месте, меняем слагаемые местами, это можно сделать, т.к. в скобке сумма, название функции не изменяется, остается косинус, скобка определяет угол I четверти, косинус в этой четверти имеет знак «+»).
не на первом месте, меняем слагаемые местами, это можно сделать, т.к. в скобке сумма, название функции не изменяется, остается косинус, скобка определяет угол I четверти, косинус в этой четверти имеет знак «+»).
6) 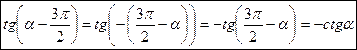 (в скобке угол
(в скобке угол 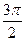 не на первом месте, чтобы поменять местами надо вынести «-» за скобки и учесть формулу
не на первом месте, чтобы поменять местами надо вынести «-» за скобки и учесть формулу 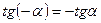 , название функции изменяется на котангенс, скобка определяет угол III четверти, тангенс в этой четверти имеет знак «+», поэтому минус сохранился).
, название функции изменяется на котангенс, скобка определяет угол III четверти, тангенс в этой четверти имеет знак «+», поэтому минус сохранился).
7) 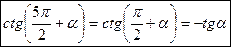 (в скобке угол
(в скобке угол 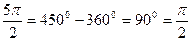 , название функции изменяется на тангенс, скобка
, название функции изменяется на тангенс, скобка 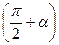 определяет угол II четверти, котангенс в этой четверти имеет знак «-»).
определяет угол II четверти, котангенс в этой четверти имеет знак «-»).
Пример 2:Вычислить значения тригонометрических функций, которых нет в таблице, с применением формул приведения (углы расписать на сумму или разность через углы 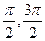 ,
, 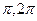 и один из острых табличных углов 300, 600, 450).
и один из острых табличных углов 300, 600, 450).
1) 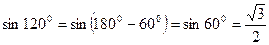 или
или 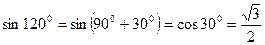
2) 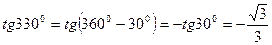 или
или 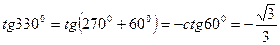
3) 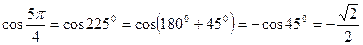 (в скобке угол
(в скобке угол 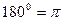 , название функции не изменяется, остается косинус, угол 2250 - III четверть, косинус в этой четверти имеет знак «-»).
, название функции не изменяется, остается косинус, угол 2250 - III четверть, косинус в этой четверти имеет знак «-»).
Задание:
1) Применить формулы приведения:
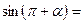
| 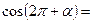
|
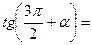
| 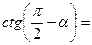
|
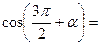
| 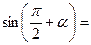
|
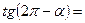
| 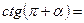
|
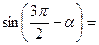
| 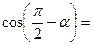
|
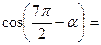
| 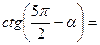
|
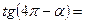
| 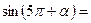
|
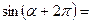
| 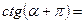
|
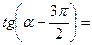
| 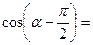
|
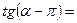
| 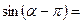
|
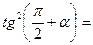
| 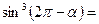
|
2) Выполнить указанные номера из учебника (под ред. Алимова):
стр. 159, 160 № 525, 526, 529(4,6).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|