ФОРМУЛЫ СТОКСА И ОСТРОГРАДСКОГО

ФОРМУЛЫ СТОКСА И ОСТРОГРАДСКОГО

ПЛАН ЛЕКЦИИ

I. Формула Стокса

II. Формула Остроградского

I. Формула Стокса. Эта формула устанавливает связь между интегралом по поверхности S и криволинейным интегралом по границе L этой поверхности.

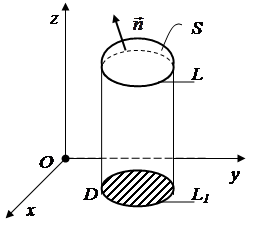Пусть поверхность S может быть задана уравнением 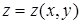.Границу поверхности S обозначим L. Положительное направление единичной нормали 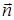выберем так, чтобы она образовывала с положительным направлением оси Oz острый угол. Направляющие косинусы нормали в этом случае вычисляются по соотношениям (7).

Пусть в пространственной области, содержащей поверхность S, задана функция 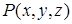, непрерывная вместе со своими частными производными. Рассмотрим криволинейный интеграл по кривой L: 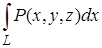. На линии L существует связь 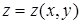, следовательно, 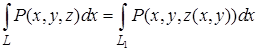– интеграл по линии L₁ – проекции линии L в плоскость Oxy. Преобразуем этот интеграл по формуле Грина, положив 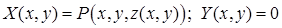, и получим

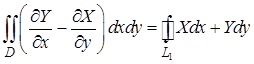
или

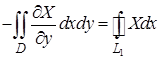, так как .

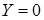На основании выражения для производной сложной функции имеем

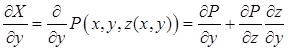Тогда

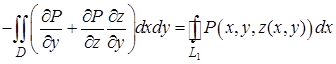
или

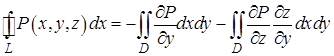Интегралы, стоящие в правой части, можно представить как поверхностные, если учесть, что :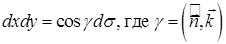

, .

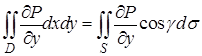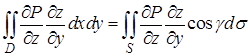С учётом соотношений (7)

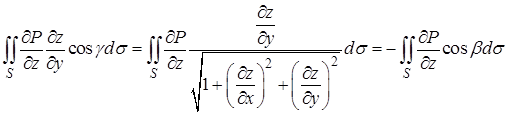Тогда получаем, что

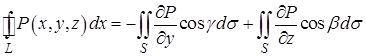. (10)

Направление обхода контура L должно быть согласовано с выбранным положительным направлением нормали 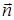: если смотреть с конца нормали, то обход контура L надо видеть против часовой стрелки.

Аналогично получим и следующие выражения для интегралов:

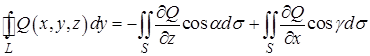, (10¢)

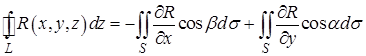. (10¢¢)

Складывая левые и правые части формул (10), (10¢), (10¢¢), получим формулу Стокса:

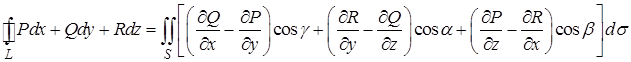
или

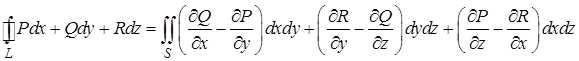. (11)

Если поверхность S есть часть плоскости, параллельной плоскости Oxy, то 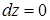и из формулы Стокса получаем формулу Грина как частный случай (11).

II. Формула Остроградского. Эта формула связывает тройной интеграл по пространственной области 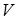с поверхностным интегралом по поверхности, ограничивающей область .

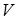В пространстве задана область 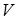, ограниченная замкнутой поверхностью S, проектирующаяся в плоскость Oxy в правильную область D. В пространственной области 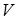заданы функции 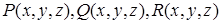, непрерывные вместе со своими частными производными.

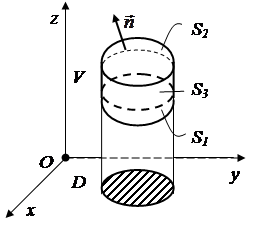Пусть поверхность S можно разбить на три части S₁, S₂и S₃ так, что

;

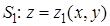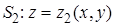S₃ – цилиндрическая поверхность с образующей, параллельной оси Oz.

Рассмотрим интеграл

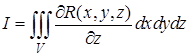Произведём интегрирование по z:

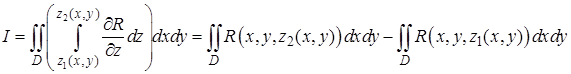Выберем направление нормали к поверхности S внешнее по отношению к области 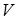, тогда 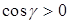на поверхности S₂, 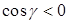на S₁ и 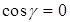на цилиндрической поверхности S₃.

Двойные интегралы, стоящие в правой части последнего равенства, равны соответствующим интегралам по поверхности:

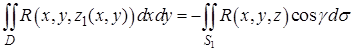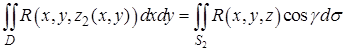Тогда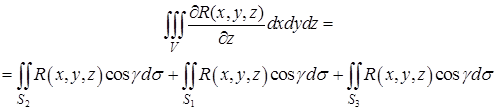

или

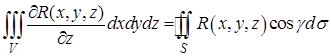, (12)

так как .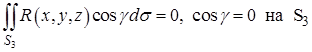

Аналогично можно получить соотношения

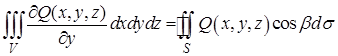, (12¢)

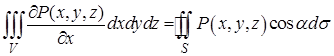. (12¢¢)

Складывая почленно формулы (12), (12¢), (12¢¢), получим формулу Остроградского:

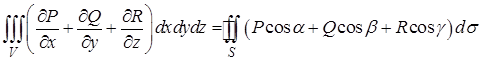. (13)

Если функции 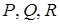представляют собой составляющие вектора скорости жидкости, протекающей через область 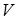, то формуле Остроградского можно дать гидромеханическую интерпретацию: изменение количества жидкости внутри области 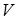обусловлено потоком жидкости через ограничивающую 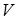поверхность.