
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формулы понижения степени, их доказательство
Формулы понижения степени
Формулы понижения степени, их доказательство
Запишем формулы понижения степени со второй по четвертую для синуса и косинуса, ниже приведем их вывод. А после этого дадим общий вид формул понижения степени.

Теперь перейдем к выводу этих формул понижения степени.
Формулы понижения для квадрата синуса и косинуса напрямую следуют из формул двойного угла вида 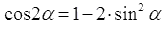 и
и 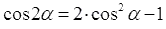 . Записанные равенства достаточно лишь разрешить относительно синуса в квадрате и косинуса в квадрате, что даст формулы
. Записанные равенства достаточно лишь разрешить относительно синуса в квадрате и косинуса в квадрате, что даст формулы 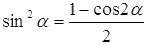 и
и 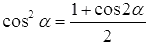 соответственно.
соответственно.
Здесь стоит отметить, что формулы понижения степени для синуса и косинуса в квадрате совпадают с формулами синуса и косинуса половинного угла.
Двигаемся дальше.
Если формулы тройного угла вида 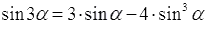 и
и 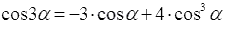 разрешить относительно синуса в кубе и косинуса в кубе, то получатся формулы понижения степени
разрешить относительно синуса в кубе и косинуса в кубе, то получатся формулы понижения степени  и
и  соответственно.
соответственно.
Доказать формулы понижения с четвертой степени вида  и
и  можно, дважды обратившись к формулам понижения синуса и косинуса в квадрате:
можно, дважды обратившись к формулам понижения синуса и косинуса в квадрате:
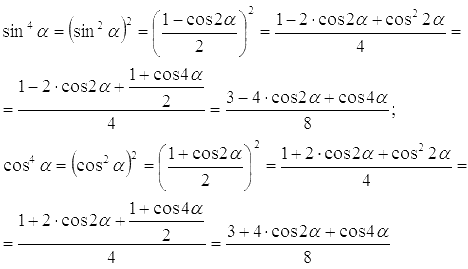
Пришло время записать общий вид формул понижения степени. Для четных показателей степени (то есть, для n=2, 4, 6, …) они имеют вид 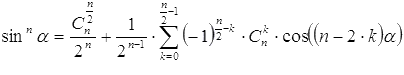 и
и 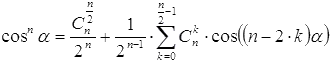 ,
,
а для нечетных (то есть, для n=3, 5, 7, …) - вид 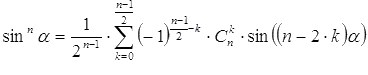 и
и 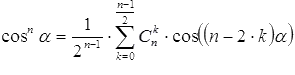 , где
, где  - число сочетаний из p элементов по q.
- число сочетаний из p элементов по q.
Покажем, как использовать формулы понижения степени общего вида на конкретном примере. Запишем с их помощью формулу понижения степени для синуса в кубе. Так как показатель степени 3 является нечетным числом, то нужно воспользоваться формулой 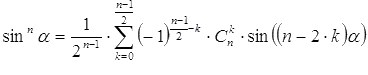 , приняв n=3. Для n=3 имеем
, приняв n=3. Для n=3 имеем
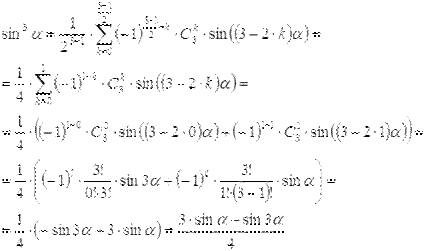
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|