Хелпикс

Главная

Контакты

Случайная статья



Формулы сложения. sin(α + β) = sinα·cosβ + cosα·sinβ;. sin(α − β) = sinα·cosβ − cosα·sinβ;. cos(α + β) = cosα·cosβ − sinα·sinβ;. cos(α −



Формулы сложения

Формулами сложения называют формулы, выражающие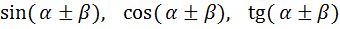

sin(α + β) = sinα·cosβ + cosα·sinβ;

sin(α − β) = sinα·cosβ − cosα·sinβ;

cos(α + β) = cosα·cosβ − sinα·sinβ;

cos(α − β) = cosα·cosβ + sinα·sinβ;


tg(α + β) =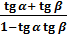


tg(α − β) =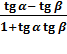

 

  1. Вычислить 

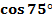
По формуле косинус суммы находим

=

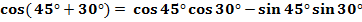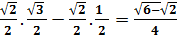
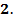Вычислить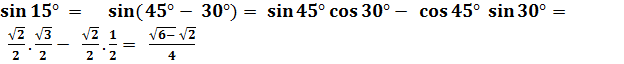 

3.Найти значение выражения:

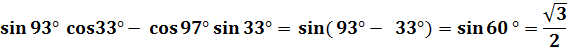
4.Вычислить: 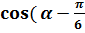     ) , есл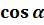и   =  и                                                                                      )=  = -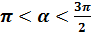

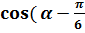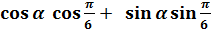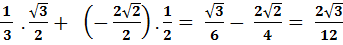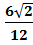
Найдем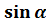

Воспользуемся основным тригонометрическим тождеством

sin2 α + cos2 α = 1.

Эта формула связывает синус и косинус одного угла. Теперь, зная косинус, мы легко найдем синус. Достаточно извлечь квадратный корень:

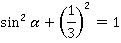
Упростив, получим:

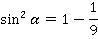
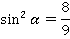
Тогда:

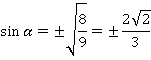
Мы получили два возможных значения синуса, т.к. 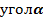 принадлежит третьей четверти, то значение 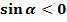, значит    =-

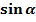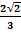
Подставим значения  в формулу и вычислим значение выражения.

Выполнить самостоятельно:

1. №481(1,3), №482, №485, №483(1), №486(2)

2.»Учи.ру» тема « Тригонометрические формулы» карточки «Формулы сложения»
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.