
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Показательная функция, её свойства и график
Показательная функция, её свойства и график
Построим графики функций 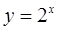 и
и 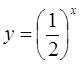 .
.
Составим таблицу значений для функции 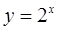 :
:
| х | -3 | -2 | -1 | ||||
| у | 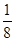
| 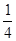
| 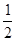
|
Составим таблицу значений для функции 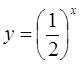 :
:
| х | -3 | -2 | -1 | ||||
| у | 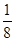
| 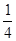
| 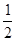
|
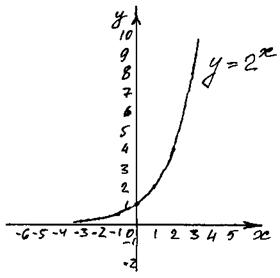
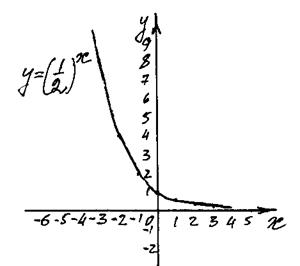
Функция, заданная формулой 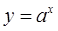 (где a > 0,
(где a > 0, 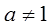 ), называется показательной функцией с основанием а.
), называется показательной функцией с основанием а.
Основные свойства показательной функции.
Свойство 1.Область определения – множество R действительных чисел.
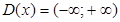 .
.
Свойство 2.Область значений – множество R+ всех положительных действительных чисел. 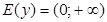 .
.
Свойство 3.При a > 1 функция возрастает на всей числовой прямой; при 0 < a < 1 функция убывает на множестве R.
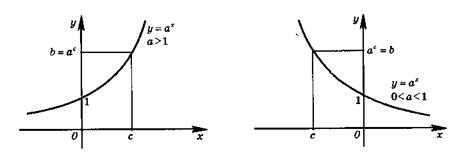
Свойство 4.При любых действительных значениях х и у справедливы неравенства:
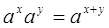 ;
; 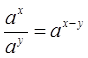 ;
; 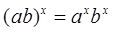 ;
; 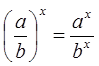 ;
;
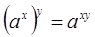 .
.
Пример 1. Вычислите значение выражения 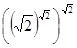 .
.
Решение.
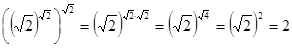 .
.
Ответ: 2.
Домашнее задание.
№ 448. Вычислите значение выражения: б) 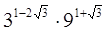 ; в)
; в) 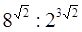 ; г)
; г) 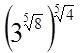 .
.
№ 448. Упростите выражение: а) 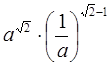 ; б)
; б) 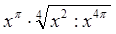 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|