
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Инструкция по выполнению задания
| Дата | |
| Группа | 118-1 |
| Дисциплина | Техническая механика |
| Форма занятия (лекция/ лабораторная работа/ практическое занятие/ дифференцированный зачет/свой вариант) | Лекция |
| Тема | Кручение. Основные понятия. Крутящий момент. |
| Содержание занятия | Кручение. Основные понятия. Внешние силы, вызывающие кручение прямого бруса. Крутящий момент. Гипотезы при кручении. |
| Форма обратной связи | В рабочей тетради ответить на контрольные вопросы. Фотографию выполненных заданий прислать на электронную почту baranovang1978.baranova@yandex. |
| Сроки выполнения | К следующему уроку |
Инструкция по выполнению задания
1. Изучить по учебнику Олофинская В.П. Техническая механика: Курс лекций с вариантами практических заданий: М.: ФОРУМ: ИНФРА-М, 2016 г. тему 2.5 Кручение. Внутренние силовые факторы при кручении (лекция 26).
2. Выполнить в рабочей тетради конспект темы «Кручение. Основные понятия. Крутящий момент».
3. В рабочей тетради ответить на контрольные вопросы. Фотографию выполненных заданий прислать на электронную почту baranovang1978.baranova@yandex.
Тема 2.5 Кручение
2.5.1 Основные понятия. Крутящий момент
Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.
Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его продольной оси (рис.1).
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.
В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).
При этом образующие бруса искривляются и разворачиваются на угол γ, называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения). Длина бруса и размеры поперечного сечения при кручении не изменяются.
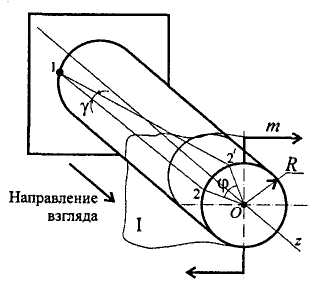
γ – угол сдвига;
φ – угол закручивания.
Связь между угловыми деформациями определяется соотношением:

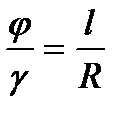
где l- длина бруса; R- радиус сечения.
Длина бруса значительно больше радиуса сечения, следовательно, φ>>γ.
Угловые деформации при кручении рассчитываются в радианах.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|