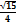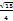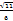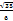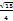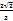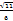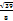Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB = 15.

Геометрия. Задания 23, 25 ФЛЭШ- карточки. ФИПИ

Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведённую к гипотенузе.	Катет и гипотенуза прямоугольного треугольника равны 21 и 75. Найдите высоту, проведённую к гипотенузе.	Точка H является основанием высоты, проведённой из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если AH = 9, AC=36.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 5, CK = 14	Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC= 11, а расстояние от точки K до стороны AB равно 3.	Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.	Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 10.	Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD = 36.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 11, AС=44, NС=18.	Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 12, СD = 48, AС = 35.	Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 24, а расстояния от центра окружности до хорд AB и CD равны соответственно 16 и 12.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 14, CD = 48, а расстояние от центра окружности до хорды AB равно 24.	Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK = 11.	Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=14
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 36, а сторона BC в 1,8 раза меньше стороны AB.	Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=16, а сторона AC в 1,6 раза больше стороны BC.	92. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB = 15.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=9, AC=12.	Углы B и C треугольника ABC равны соответственно 63° и 87°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 11.	В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.	В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.	Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.	Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=10, а углы B и C четырёхугольника равны соответственно 112° и 113°.	Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.	В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.	В треугольнике ABC известны длины сторон AB=40, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.	Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.	В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника ABC.
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC. Найдите AH.	Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=	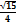На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC. Найдите AH.
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=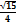

Геометрия Все Задания 23 и 25. ФИПИ


1. Катеты прямоугольного треугольника равны 15 и 20.Найдите высоту, проведённую к гипотенузе	равны 18 и 24
	равны 21 и 28.
	равны 10 и 24.
	равны 15 и 36.

2. Катет и гипотенуза прямоугольного треугольника равны 21 и 75. Найдите высоту, проведённую к гипотенузе.	равны 16 и 34.
	равны 24 и 51
	равны 35 и 125.
	равны 20 и 52.

3.Точка H является основанием высоты, проведённой из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если AH = 9, AC=36.	если AH=6, AC=24.
	если AH=7, AC=28.
	если AH=8, AC=32.
	если AH=5, AC=45.
	если AH=10, AC=40.
	если AH=5, AC=20.
	если AH=3, AC=27.
	если AH=4, AC=16.
	если AH=3, AC=12.

4.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 5, CK = 14	если BK=4, CK=19.
	если BK=9, CK=15.
	если BK=11, CK=20.
	если BK=10, CK=18
	если BK=12, CK=16.

5.Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC= 11, а расстояние от точки K до стороны AB равно 3.	если BC=19, а расстояние от точки K до стороны AB равно 7.
	если BC=12, а расстояние от точки K до стороны AB равно 9.
	если BC=19, а расстояние от точки K до стороны AB равно 10.
	если BC=17, а расстояние от точки K до стороны AB равно 10.
	если BC=18, а расстояние от точки K до стороны AB равно 1.
	если BC=7, а расстояние от точки K до стороны AB равно 4.
	если BC=2, а расстояние от точки K до стороны AB равно 8.
	если BC=6, а расстояние от точки K до стороны AB равно 6.
	если BC=2, а расстояние от точки K до стороны AB равно 1.

6.Расстояние от точки пересечения диагоналей ромба до одной из его сторонравно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.	равно 10, а одна из диагоналей ромба равна 40
	равно 11, а одна из диагоналей ромба равна 44
	равно 12, а одна из диагоналей ромба равна 48.
	равно 13, а одна из диагоналей ромба равна 52
	равно 14, а одна из диагоналей ромба равна 56.
	равно 16, а одна из диагоналей ромба равна 64
	равно 17, а одна из диагоналей ромба равна 68
	равно 18, а одна из диагоналей ромба равна 72
	равно 19, а одна из диагоналей ромба равна 76

7.Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.	на отрезки DH=8 и CH=2.
	на отрезки DH=12 и CH=1.
	на отрезки DH=12 и CH=3.
	на отрезки DH=16 и CH=4.
	на отрезки DH=20 и CH=5
	на отрезки DH=24 и CH=1.
	на отрезки DH=24 и CH=2
	на отрезки DH=21 и CH=8.
	на отрезки DH=24 и CH=6.

8.Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB,если AF = 24, BF = 10.	если AF=12, BF=5.
	если AF=12, BF=9.
	если AF=15, BF=8.
	если AF=16, BF=12.
	если AF=20, BF=15.
	если AF=24, BF=7.
	если AF=21, BF=20.
	если AF=24, BF=18.
	если AF=32, BF=24.

9.Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD = 36.	соответственно 60° и 135°, а CD=24.
	соответственно 30° и 135°, а CD=29.
	соответственно 30° и 135°, а CD=17.
	соответственно 60° и 150°, а CD=33.

10.Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 11, AС=44, NС=18.	если MN=17, AC=51, NC=32.
	если MN=13, AC=65, NC=28.
	если MN=14, AC=21, NC=10.
	если MN=22, AC=55, NC=36.
	если MN=15, AC=25, NC=22.
	если MN=16, AC=20, NC=15.
	если MN=12, AC=42, NC=25.
	если MN=18, AC=42, NC=40.
	если MN=20, AC=35, NC=39.

11.Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC,если AB = 12, СD = 48, AС = 35.	если AB=14, DC=42, AC=52.
	если AB=13, DC=65, AC=42.
	если AB=11, DC=22, AC=27.
	если AB=10, DC=25, AC=56.
	если AB=16, DC=24, AC=25.
	если AB=15, DC=30, AC=39.
	если AB=18, DC=54, AC=48.
	если AB=14, DC=56, AC=40.
	если AB=11, DC=55, AC=30.

12.Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 24, а расстояния от центра окружности до хорд AB и CD равны соответственно 16 и 12.	если AB=10, а расстояния равны соответственно 12 и 5.
	если AB=12, а расстояния равны соответственно 8 и 6.
	если AB=18, а расстояния равны соответственно 12 и 9.
	если AB=16, а расстояния равны соответственно 15 и 8.

13.Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 14, CD = 48, а расстояние от центра окружности до хорды AB равно 24.	если AB=30, CD=40, а расстояние равно 20.
	если AB=20, CD=48, а расстояние равно 24.
	если AB=40, CD=42, а расстояние равно 21.
	если AB=36, CD=48, а расстояние равно 24.

14.Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK = 11.	если PK=15.
	если PK=14.
	если PK=13.
	если PK=12.

15.Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=14	если BH=13.
	если BH=12.
	если BH=15.
	если BH=11.

16.Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 36, а сторона BC в 1,8 раза меньше стороны AB.	если AP=21, а сторона BC в 1,5 раза меньше
	если AP=9, а сторона BC в 3 раза меньше
	если AP=34, а сторона BC в 2 раза меньше
	если AP=30, а сторона BC в 1,2 раза меньше

17.Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=16, а сторона AC в 1,6 раза больше стороны BC.	если AK=14, а сторона AC в 2 раза больше.
	если AK=18, а сторона AC в 1,2 раза больше
	если AK=6, а сторона AC в 1,5 раза больше
	если AK=7, а сторона AC в 1,4 раза больше

18.Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB = 15.

если диаметр окружности равен 3,6, а AB=8.

если диаметр окружности равен 6,4, а AB=6.

если диаметр окружности равен 8,4, а AB=4.

если диаметр окружности равен 15, а AB=4.

19.Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=9, AC=12.

если AB=3, AC=5.

если AB=2, AC=8.

если AB=1, AC=5.

если AB=3, AC=9.

20.Углы B и C треугольника ABC равны соответственно 63° и 87°. Найдите BC,если радиус окружности, описанной около треугольника ABC,равен 11.

равны 71° и 79°, если радиус равен 8.

равны 73° и 77°, если радиус равен 9.

равны 61° и 89°, если радиус равен 10.

равны 62° и 88°, если радиус равен 12.

равны 64° и 86°, если радиус равен 13.

равны 65° и 85°, если радиус равен 14.

равны 66° и 84°, если радиус равен 15.

равны 67° и 83°, если радиус равен 16.

равны 72° и 78°, если радиус равен 17.

21.В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.

в отношении 5:4, если BC=18.

в отношении 5:3, если BC=16.

в отношении 41:40, если BC=18.

в отношении 17:15, если BC=16.

в отношении 5:4, если BC=12.

в отношении 5:4, если BC=6

в отношении 13:12, если BC=20.

в отношении 25:24, если BC=14.

в отношении 13:12, если BC=10.

22.В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.

соответственно равны 13, 6 и 5.

соответственно равны 13, 7 и 5.

соответственно равны 13, 8 и 5.

соответственно равны 13, 9 и 5.

соответственно равны 25, 13 и 7.

соответственно равны 25, 14 и 7.

соответственно равны 25, 15 и 7.

соответственно равны 25, 17 и 7.

соответственно равны 25, 19 и 7.

23. В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

периметр равен 80, а площадь равна 320,

периметр равен 220, а площадь равна 2420

периметр равен 40, а площадь равна 80

периметр равен 180, а площадь равна 1620

периметр равен 100, а площадь равна 500

периметр равен 20, а площадь равна 20

периметр равен 160, а площадь равна 1280

периметр равен 200, а площадь равна 2000

24.Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.

если AD=25, BC=15, CF:DF=3:2.

если AD=44, BC=24, CF:DF=3:1.

если AD=33, BC=18, CF:DF=2:1.

если AD=45, BC=20, CF:DF=4:1.

если AD=36, BC=18, CF:DF=7:2.

если AD=35, BC=21, CF:DF=5:2.

если AD=48, BC=16, CF:DF=5:3.

если AD=45, BC=27, CF:DF=5:4.

если AD=50, BC=30, CF:DF=7:3.

25.Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.

равны 47° и 43°, а отрезки равны 16 и 14.

равны 39° и 51°, а отрезки равны 19 и 3

равны 50° и 40°, а отрезки равны 15 и 13.

равны 53° и 37°, а отрезки равны 6 и 2

равны 86° и 4°, а отрезки равны 4 и 1.

равны 18° и 72°, а отрезки равны 15 и 4

равны 80° и 10°, а отрезки равны 20 и 17

равны 39° и 51°, а отрезки равны 19 и 17.

равны 7° и 83°, а отрезки равны 14 и 11

26.Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=10, а углы B и C четырёхугольника равны соответственно 112° и 113°.

если BC=12, а углы B и C равны соответственно 115° и 95°.

если BC=9, а углы B и C равны соответственно 116° и 94°.

если BC=19, а углы B и C равны соответственно 95° и 115°

если BC=8, а углы B и C равны соответственно 129° и 96°.

если BC=11, а углы B и C равны соответственно 126° и 99°.

если BC=6, а углы B и C равны соответственно 124° и 116°.

если BC=14, а углы B и C равны соответственно 110° и 100°.

если BC=3, а углы B и C равны соответственно 94° и 131°.

если BC=18, а углы B и C равны соответственно 132° и 93°.

27.Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.

со сторонами AB=5 и CD=17

со сторонами AB=39 и CD=12

со сторонами AB=43 и CD=4

со сторонами AB=34 и CD=22

со сторонами AB=11 и CD=41

со сторонами AB=44 и CD=8

со сторонами AB=12 и CD=30

со сторонами AB=39 и CD=6

со сторонами AB=40 и CD=1

28.Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

радиусов 45 и 55

радиусов 42 и 84

радиусов 4 и 60

радиусов 45 и 90

радиусов 36 и 45

радиусов 33 и 99

радиусов 12 и 20

радиусов 44 и 77

радиусов 22 и 99

29.В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.

соответственно 18 и 6, если AB=10.

соответственно 33 и 11, если AB=20.

соответственно 32 и 24, если AB=7.

соответственно 34 и 14, если AB=12.

соответственно 48 и 2, если AB=13.

соответственно 36 и 12, если AB=13.

соответственно 32 и 4, если AB=14.

соответственно 34 и 2, если AB=24.

соответственно 28 и 4, если AB=15.

30.В треугольнике ABC известны длины сторон AB=40, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.

AB=30, AC=100,

AB=84, AC=98

AB=30, AC=100

AB=12, AC=72,

AB=36, AC=54

AB=28, AC=56,

AB=60, AC=80,

AB=15, AC=25

AB=14, AC=98

31.В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.

если AD=14, BC=7.

если AD=8, BC=4.

если AD=8, BC=7.

если AD=4, BC=2.

если AD=12, BC=9.

если AD=20, BC=15.

если AD=12, BC=10.

если AD=6, BC=5.

если AD=20, BC=10.

32.Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41,
а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

соответственно 24 и 25, а основание BC равно 9.

соответственно 10 и 26, а основание BC равно 1.

соответственно 20 и 29, а основание BC равно 4.

соответственно 6 и 10, а основание BC равно 1

соответственно 12 и 13, а основание BC равно 4.

соответственно 16 и 34, а основание BC равно 2.

соответственно 4 и 5,а основание BC равно 1.

соответственно 28 и 35, а основание BC равно 7.

соответственно 8 и 10, а основание BC равно 2.

33.В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника ABC.

равную 44.

равную 16

равную 20.

равную 8.

равную 24.

равную 28

равную 32.

равную 36

равную 40.

34.На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC. Найдите AH.

AD=9, MD=6,

AD=9, MD=3,

AD=90, MD=69

AD=15, MD=12,

AD=80, MD=64,

AD=16, MD=4,

AD=72, MD=18,

AD=81, MD=9,

AD=45, MD=15,

35.Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 4 и 15 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=

соответственно 12 и 21 от вершины A., если cos∠BAC=

соответственно 8 и 30 от вершины A., если cos∠BAC=

соответственно 18 и 22 от вершины A., если cos∠BAC=

соответственно 18 и 40 от вершины A., если cos∠BAC=

соответственно 9 и 35 от вершины A., если cos∠BAC=

соответственно 12 и 45 от вершины A., если cos∠BAC=

соответственно 9 и 32 от вершины A, если cos∠BAC=

соответственно 24 и 42 от вершины A., если cos∠BAC=

соответственно 36 и 44 от вершины A., если cos∠BAC=

соответственно 16 и 39 от вершины A., если cos∠BAC=

соответственно 9 и 11 от вершины A., если cos∠BAC=