ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Суммой двух событий A и B называется событие C=A+B, состоящее в появлении или события A, или события B, или обоих вместе. Ключевое слово «или» («либо»).

Произведением двух событий A и B называется событие C=AB, состоящее в совместном выполнении события A и события B. Ключевое слово «и».

Два события называются несовместными, если они не могут появиться одновременно.

Теорема сложения.

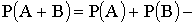для несовместных событий;

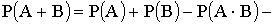для совместных событий.

Два события называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого.

Условной вероятностью 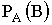называют вероятность события A, вычисленную в предположении, что событие B уже наступило.

Теорема умножения.

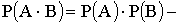для независимых событий;

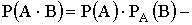для зависимых событий.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

В урне 3 красных и 4 белых шара, 5 красных, 2 белых и 6 черных кубов. Из урны наудачу вынимается одно изделие. Найти вероятность того, что выбранное изделие а) либо белое, либо черное; б) либо красное, либо куб.

РЕШЕНИЕ: а) Рассмотрим события:

A — изделие белое; 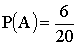, так как всего изделий 20, а белых шесть.

B — изделие черное, .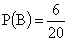

Событие C — изделие либо белое, либо черное можно представить как сумму событий A и B. Следовательно, .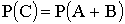

События A и B несовместны, так как вынутое изделие не может быть одновременно и белым и черным. Тогда .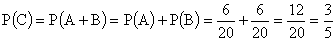

б) Введем события

D — изделие красное; ;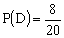

E — изделие куб; ;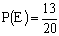

F — изделие либо красное, либо куб; .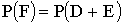

События D и E совместны, так как вынутое изделие может оказаться красным кубом 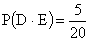. Тогда

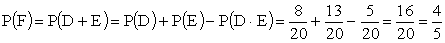ПРИМЕР 13.2.27. В ящике 10 деталей, 3 из которых бракованные. Наудачу вынимают два изделия. Найти вероятность того, что оба изделия бракованные, если первое изделие: а) возвращается в ящик; б) в ящик не возвращается.

РЕШЕНИЕ. Введем события

A — первое изделие бракованное,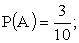

B — второе изделие бракованное,

C — оба изделия бракованные.

Событие C представляет собой произведение событий A и B; C=AB.

а) Если первое изделие возвращается в ящик, то 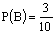вне зависимости от того, какое изделие было первое, то есть A и B — независимые события. Тогда .

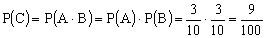б) Если изделие не возвращается, то вероятность события B будет меняться в зависимости от того, какое изделие было вынуто первым (бракованное или небракованное). Найдем вероятность события B в предположении, что первое изделие оказалось бракованным. 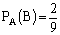, так как всего осталось 9 изделий, два из которых бракованные. Тогда

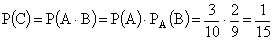ПРИМЕР 13.2.28. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет: а) только один из стрелков; б) хотя бы один стрелок.

РЕШЕНИЕ. Рассмотрим события

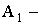первый стрелок попал; ;

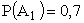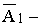первый стрелок промахнулся; ;

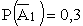второй стрелок попал; ;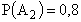

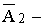второй стрелок промахнулся; .

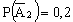а) Событие B попал только один стрелок, используя алгебру событий, можно представить в виде
.

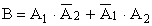Тогда по теореме сложения вероятностей несовместных и умножения независимых событий имеем:

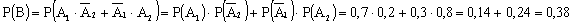б) Событие C попал хотя бы один стрелок можно представить как сумму двух несовместных событий: B — попал только один стрелок и D- попали оба стрелка

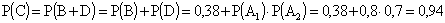Однако вероятность события C можно найти другим способом. Рассмотрим событие 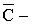оба промахнулись,

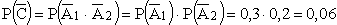Тогда .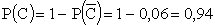

Решить самостоятельно

В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.

В урне белых и черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара будут белыми, если выемку производить: а) с возвращением; б) без возвращения.

В мешке смешаны нити, среди которых 30% белых, а остальные – красные. Определить вероятности того, что вынутые наудачу две нити будут а) одного цвета; б) разных цветов.

Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы за определенный промежуток времени первого, второго и третьего элемента соответственно равны 0,6;0,7;0,8. Найти вероятности того, что за это время безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента; г) хотя бы два элемента.

Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.