
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Повторение. Расчеты по формулам и нахождение геометрических величин.
Повторение. Расчеты по формулам и нахождение геометрических величин.
1)Площадь параллелограмма 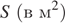 можно вычислить по формуле
можно вычислить по формуле 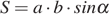 , где
, где  — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и
— стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и 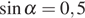 .
.
2) Длину окружности 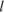 можно вычислить по формуле
можно вычислить по формуле 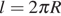 , где
, где 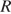 — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать
— радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать  ).
).
3) Площадь ромба 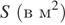 можно вычислить по формуле
можно вычислить по формуле 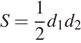 , где
, где 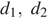 — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ
— диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ 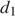 , если диагональ
, если диагональ 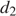 равна 30 м, а площадь ромба 120 м2.
равна 30 м, а площадь ромба 120 м2.
4) Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле  , где
, где 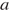 и
и 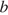 — катеты, а
— катеты, а 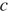 — гипотенуза треугольника. Пользуясь этой формулой, найдите
— гипотенуза треугольника. Пользуясь этой формулой, найдите 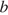 , если
, если 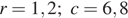 и
и  .
.
5) Из закона всемирного тяготения 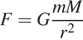 выразите массу
выразите массу 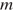 и найдите её величину (в килограммах), если
и найдите её величину (в килограммах), если 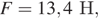
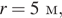
 и гравитационная постоянная
и гравитационная постоянная 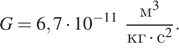
6) Закон Кулона можно записать в виде 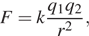 где
где 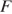 — сила взаимодействия зарядов (в ньютонах),
— сила взаимодействия зарядов (в ньютонах), 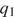 и
и 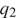 — величины зарядов (в кулонах),
— величины зарядов (в кулонах), 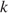 — коэффициент пропорциональности (в Н·м2/Кл2 ), а
— коэффициент пропорциональности (в Н·м2/Кл2 ), а 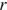 — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда
— расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда 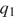 (в кулонах), если
(в кулонах), если 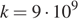 Н·м2/Кл2,
Н·м2/Кл2, 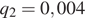 Кл,
Кл, 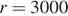 м, а
м, а 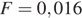 Н.
Н.
7) Период колебания математического маятника 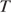 (в секундах) приближенно можно вычислить по формуле
(в секундах) приближенно можно вычислить по формуле 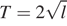 , где
, где 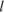 — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
— длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
8) Радиус описанной около треугольника окружности можно найти по формуле  , где
, где 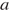 — сторона треугольника,
— сторона треугольника, 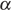 — противолежащий этой стороне угол, а
— противолежащий этой стороне угол, а 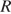 — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите
— радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите  , если
, если 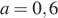 , а
, а 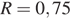 .
.
9)
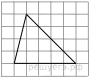
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.
10)
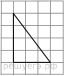
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
11)
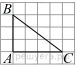 Найдите тангенс угла
Найдите тангенс угла  треугольника
треугольника 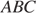 , изображённого на рисунке.
, изображённого на рисунке.
12)
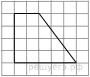
Найдите площадь и синус острого угла трапеции, изображённой на рисунке.
13)
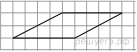
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь и косинус острого угла, умноженный на 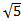
14)
 Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.
Площадь одной клетки равна 1. Найдите площадь закрашенной фигуры.
15)
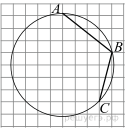
Найдите угол 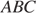
16)
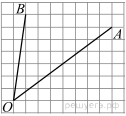
Найдите тангенс угла 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|