Законы движения планет Солнечной системы

12. Законы движения планет Солнечной системы

12.1 Пример решения задач
12.2 Вопросы

Важную роль в формировании представлений о строении Солнечной системы сыграли также законы движения планет, которые были открыты Иоганном Кеплером (1571—1630) и стали первыми естественнонаучными законами в их современном понимании. Работы Кеплера создали возможность для обобщения знаний по механике той эпохи в виде законов динамики и закона всемирного тяготения, сформулированных позднее Исааком Ньютоном. Многие ученые вплоть до начала XVII в. считали, что движение небесных тел должно быть равномерным и происходить по «самой совершенной» кривой— окружности. Лишь Кеплеру удалось преодолеть этот предрассудок и установить действительную форму планетных орбит, а также закономерность изменения скорости движения планет при их обращении вокруг Солнца.

В своих поисках Кеплер исходил из убеждения, что «в мире правит число», высказанного еще Пифагором. Он искал соотношения между различными величинами, характеризующими движение планет, — размеры орбит, период обращения, скорость. Кеплер действовал фактически вслепую, чисто эмпирически. Он пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон описанных и вписанных в орбиты планет многоугольников Иоганн Кеплер и т. д.

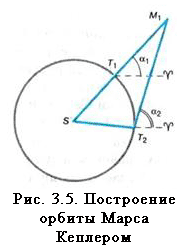Кеплеру необходимо было построить орбиты планет, перейти от экваториальной системы координат, указывающих положение планеты на небесной сфере, к системе координат, указывающих ее положение в плоскости орбиты. Он воспользовался при этом собственными наблюдениями планеты Марс, а также многолетними определениями координат и конфигураций этой планеты, проведенными его учителем Тихо Браге.Орбиту Земли Кеплер считал (в первом приближении) окружностью, что не противоречило наблюдениям. Для того чтобы построить орбиту Марса, он применил способ, который показан на рисунке 3.5.

Пусть нам известно угловое расстояние Марса от точки весеннего равноденствия во время одного из противостояний планеты — его прямое восхождение α₁, которое выражается углом Т₁М₁ где Т₁ — положение Земли на орбите в этот момент, а М₁— положение Марса. Очевидно, что спустя 687 суток (таков звездный период обращения Марса) планета придет в ту же точку своей орбиты. Если определить прямое восхождение Марса на эту дату, то, как видно из рисунка 3.5, можно указать положение планеты в пространстве, точнее, в плоскости ее орбиты. Земля в этот момент находится в точке Т₂, и, следовательно, угол T₂M₁есть не что иное, как прямое восхождение Марса — α₂. Повторив подобные операции для нескольких других противостояний Марса, Кеплер получил еще целый ряд точек и, проведя по ним плавную кривую, построил орбиту этой планеты.

Изучив расположение полученных точек, он обнаружил, что скорость движения планеты по орбите меняется, но при этом радиус-вектор планеты за равные промежутки времени описывает равные площади. Впоследствии эта закономерность получила название второго закона Кеплера.

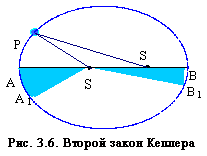Этот закон, который часто называют законом площадей, иллюстрируется рисунком 3.6. Радиус-вектором называют в данном случае переменный по своей величине отрезок, соединяющий Солнце и ту точку орбиты, в которой находится планета. АА₁ ВВ₁ и СС₁ — дуги, которые проходит планета за равные промежутки времени. Площади заштрихованных фигур равны между собой.

Согласно закону сохранения энергии, полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна во всех точках орбиты и равна полной энергии. По мере приближения планеты к Солнцу возрастает ее скорость — увеличивается кинетическая энергия, но вследствие уменьшения расстояния до Солнца уменьшается энергия потенциальная.

Установив закономерность изменения скорости движения планет, Кеплер задался целью определить, по какой кривой происходит их обращение вокруг Солнца. Он был поставлен перед необходимостью сделать выбор одного из двух возможных решений: 1) считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями (из-за ошибок наблюдений) на 8′; 2) считать, что наблюдения таких ошибок не содержат, а орбита не является окружностью. Будучи уверенным в точности наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом, при этом Солнце не располагается в центре эллипса. В результате был сформулирован закон, который называется первым законом Кеплера.

12 Следующая ⇒