Контакты

Случайная статья

Производная и дифференциал функции

Производная и дифференциал функции

Опрос.

1. Дать определения частных производных функции 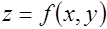по х и по у и записать символами.

2. Пояснить геометрический смысл частных производных функции .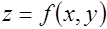

3. Дать определение и записать формулы для вычисления частных дифференциалов функции 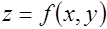по х и по у.

4. Дать определение и записать формулу для вычисления полного дифференциала функции dz.

Найти частные производные указанных функций.

1. .

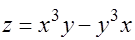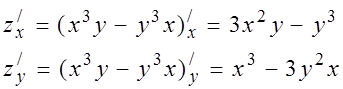
2.

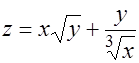
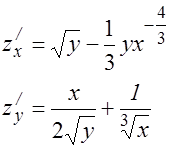
3.

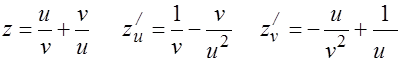
4.

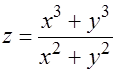
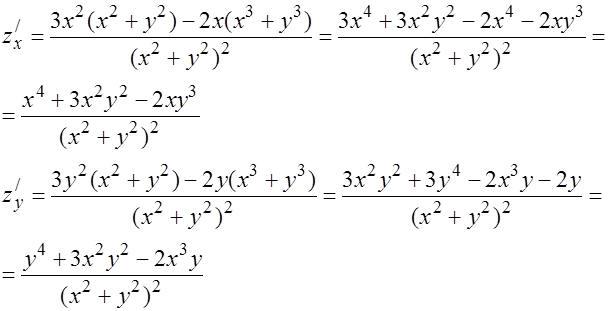
5.

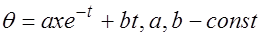
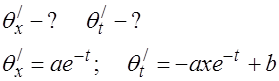
6.

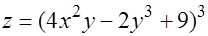
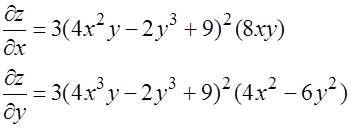
7.

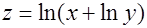
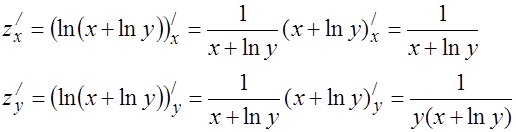
8.

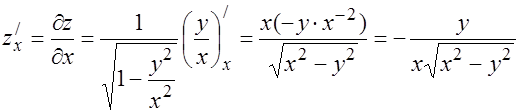
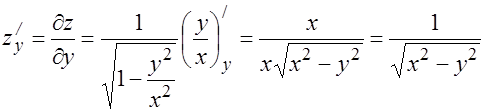
9.

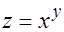
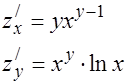
10.

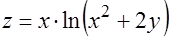
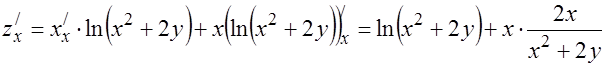
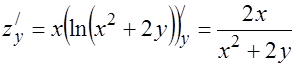
11.Проверить удовлетворяет ли указанному уравнению данная функция.

а)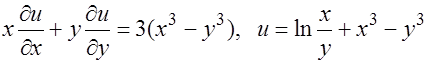

Решение.

Найдём частные производные функций

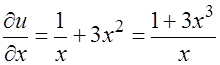
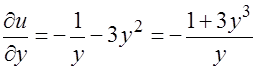
Подставим полученные выражения в уравнение:

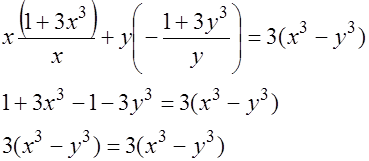
б)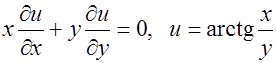

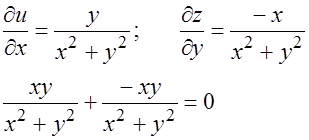
Найти полный дифференциал функций:

1.

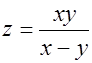
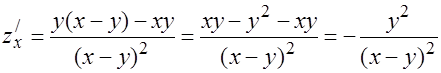
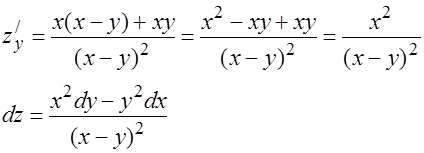
2.

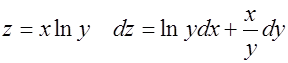
3.

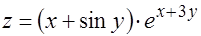
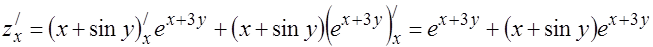
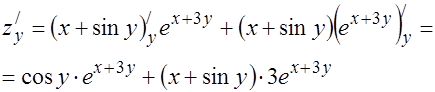
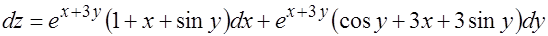
4.Найти значение полного дифференциала функции z = y/x при x = 2, y = 1,

dx = 0,1; dy = 0,2.

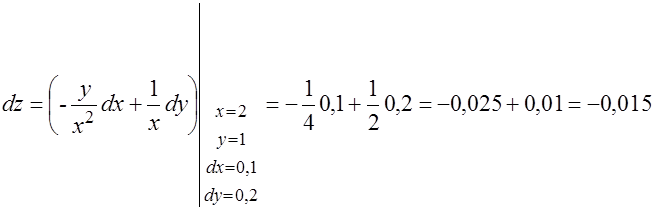
1. Производная функции 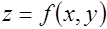в направлении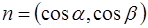

Общая формула:

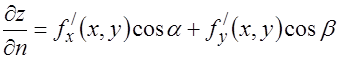
Определение:

Градиентом функции 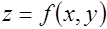в точке 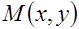называется вектор координаты, которого равны соответственно частным производным 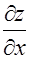и 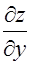, взятым в точке .

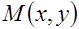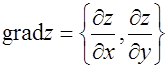
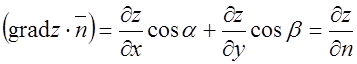
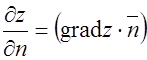
№ 4. Найдите производную функции 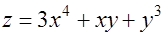в точке 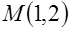по направлению, образующему с направлением оси 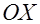угол .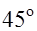

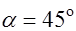
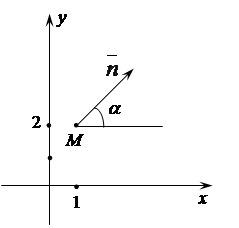, т.е.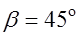

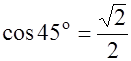
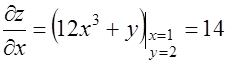
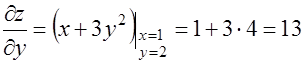
тогда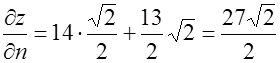

№ 2. Найти производную функции 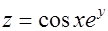в точке 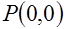в направлении, составляющем с осью OX угол .

; ; .

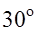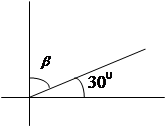
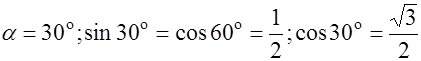
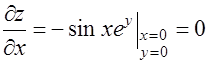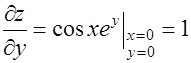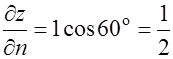№ 3. Найти производную по направлению от точки (3,1) к точке (6,5) от функции .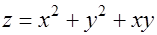

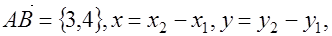
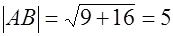
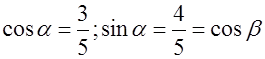
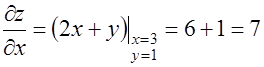
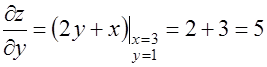
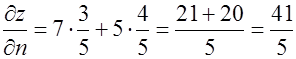
№ 4. Найти производную функции 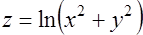в точке 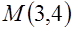в направлении градиента функции.

Р е ш е н и е:

В данном случае вектор 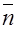совпадает с 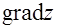в точке 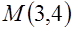и равен

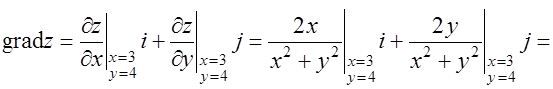
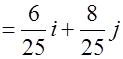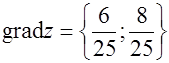, , тогда

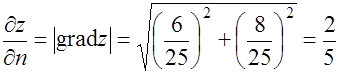
Замечание.

Градиент указывает направление наибыстрейшего роста функции в данной точке 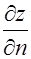в направлении градиента, имеет наибольшее значение, равное:

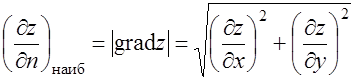
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.