
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лінійна алгебра. ПРАКТИЧНА РОБОТА №1. Системи лінійних рівнянь.. Розв'язування систем рівнянь за формулами Крамера, методом Гаусса, за допомогою оберненої матриці.. ЗАВДАННЯ ДЛЯ КОЛЕКТИВНОГО РОЗВ’ЯЗАННЯ. Розв ′язати систему лінійних рівняннь за мето
1 Лінійна алгебра
ПРАКТИЧНА РОБОТА №1
1.6 Системи лінійних рівнянь.
Розв'язування систем рівнянь за формулами Крамера, методом Гаусса, за допомогою оберненої матриці.
Навчальна мета: навчити студентів оперувати розв’язування системи лінійних рівнянь різними способами;
Розвивальна мета: розвивати інтелект студентів, уміння аналізувати, класифікувати, робити умовиводи за аналогією;
Виховна мета: формувати в студентів загально навчальні вміння: культуру мовлення, чіткість і точність думки, критичність мислення, здатність відчувати красу ідеї, методу розв'язання задачі або проблеми.
ЗАВДАННЯ ДЛЯ КОЛЕКТИВНОГО РОЗВ’ЯЗАННЯ
1. Розв ′язати систему лінійних рівняннь за формулам Крамера:
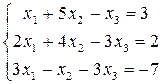
Розв’язання:
якщо 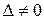 ,
, 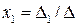 ,
,  ,
, 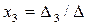 , де
, де
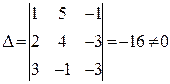 ,
,  ,
, 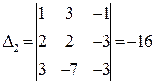 ,
, 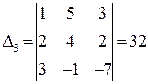
знаходимо: 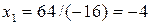 ,
, 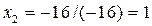 ,
, 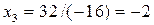
2. Розв ′язати систему лінійних рівняннь за методом Гаусса.
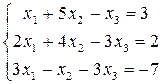
Розв’язання:
Зведемо початкову систему рівнянь к трикутному виду. Вилучимо x1 з другого й третього рівнянь. Для цього перше рівняння помножимо на 2 та віднімемо від другого, потім перше рівняння помножимо на 3 та віднімемо від третього:
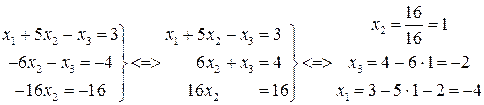
Розв’язок системи: 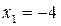 ,
, 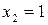 ,
, 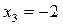 .
.
3. Розв ′язати систему лінійних рівняннь за допомогою оберненої матриці
Для знаходження розв’язку системи за допомогою оберненої матриці запишемо систему рівнянь у матричної формі 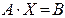 , де
, де
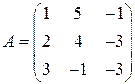 ,
,  ,
, 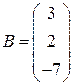 .
.
Розв’язок системи у матричної формі має вигляд 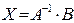 .
.
Знаходимо обернену матрицю 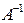 (вона існує, тому що
(вона існує, тому що 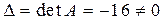 ):
):
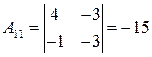 ,
, 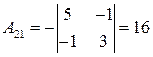 ,
, 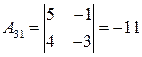
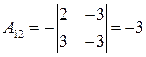 ,
, 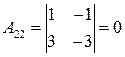 ,
, 
 ,
, 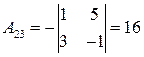 ,
, 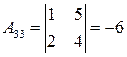
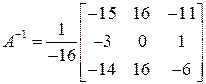
Розв’язок системи:

Отже, 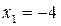 ,
, 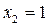 ,
, 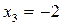
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|