ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 4

Наименование предмета:Техническая механика

Тема:Плоская система произвольно расположенных сил

Наименование работы:Приведение силы к точке плоской системы произвольно

расположенных сил

Время: 90 мин

Цель (обучающая, развивающая, воспитательная):знать способы определения главного вектора и главного момента, уметь составить уравнения равновесия для двух и более сил

Форма отчета:тетрадь

Рекомендуемая литература:А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1. Как найти равнодействующую трех сил?

2. Что можно сказать о действии сил, когда их равнодействующая равна нулю?

3. Опишите общий порядок решения задач о равновесии трех сил графическим

способом.

4. Каков общий порядок решения тех же задач аналитическим способом?

5. Какой из указанных способов более точен?

6. Приведите примеры частных случаев действия трех сил.

Указания к выполнению работы:

1. Повторить по учебнику тему «Плоская система произвольно расположенных сил»

2. Выпишите данные для вашего варианта (согласно нумерации в журнале)

№ варианта	F₁_, кН	F₂_, кН	F₃_, кН	№ варианта	F₁_, кН	F₂_, кН	F₃_, кН

3. Рассмотрите пример решения.

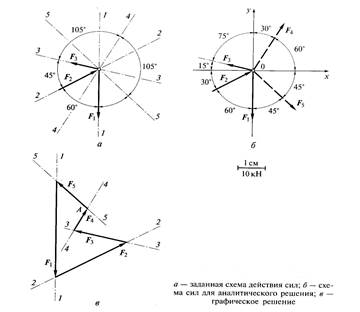
Пример. Определить величины и направления действия сил F₄ и F₅_,уравновешивающих известные силы F_1, F₂и F₃(рис. а), если F₁=40 кН, F₂=30 кН, F₃ = 20 кН.

Решение аналитическим способом (рис.б) Проводим оси координат, располагая их традиционно.

Составляем уравнение равновесия в форме:

F₂ cos 30 ^о– F₃ cos15^о+ F₄cos 60^о+F₅ cos 45^о= 0

-F₁+F₂cos 60^о+F₃cos 75^о + F₄cos 30 ^о- F₅cos 45^o= 0.

Решать задачи принято в общем виде, но в данном случае проще выделить свободные члены и коэффициенты при неизвестных F₄и F₅:

30 × 0,866 – 20 × 0,966 + F₄× 0,5 + F₅× 0,707 = 0;

- 40 + 30 × 0,5 + 20 × 0,259 +

+ F₄× 0,866 – F₅ × 0, 707 = 0.

Отсюда

0,5F₄ + 0,707 F₅= - 6, 66;

0,866 F₄ – 0,707 F₅ = 19, 82.

Такую систему проще решить не методом подстановки, а методом сложения. Сложив левую часть первого уравнения с левой частью второго, а правую часть с правой, получим

1,366 F₄= 13,16 кН.

Отсюда F₄ = 13,66 : 1,366 = 9,63 кН.

Из первого уравнения определим F₅:

- 6, 66 – 0,5F_{4 -}6, 66 – 0,5 ∙ 9, 63

F₅= -------------------- = ---------------------- = - 16, 23 кН

0,707 0,707

Ответ: F₄= 9, 63 кН, F₅= -16, 23 кН, сила направлена в сторону, противоположную показанной на рисунке.

Решение графическим способом (рис. в) Масштаб: в 1 см – 10 кН.

Откладываем в масштабе силы F₁, F₂, F₃, соблюдая заданные направления.

Через начало вектора силы F₁и конец вектора силы F₁проводим линии, параллельные линиям действия сил F₄ и F₅ до пересечения в точке А.

Измеряем полученные отрезки в сантиметрах и с учетом масштаба находим величины силы F ₄ и F₅ в килоньютонах: F₄ = 10 кН, F₅ = 16 кН.

Стрелки на векторах сил F₄и F₅ставим так, чтобы они были направлены в одну сторону при обходе многоугольника. После простановки стрелок видно, что сила F₅ направлена в сторону, противоположную показанной на рис.

Ответ: F₄= 10 кН, F₅ = 16 кН.

4. Решите свой вариант сначала аналитическим способом, а затем графическим.

5. Сравните способы решения.

6. Ответьте на вопросы.

7. Сделайте вывод.