Виды графов

⇐ ПредыдущаяСтр 2 из 2

Виды графов

Граф, состоящий из «изолированных» вершин, называется нулевым графом.

Рис 2. Нулевой граф

Граф, в которых не построены все возможные ребра, называют неполным графом.

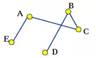
Рис. 3. Неполный граф

Граф называется полным, если каждая его вершина соединена со всеми другими вершинами графа.

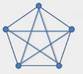
Рис. 4. Полный граф

Граф связный – если каждая вершина достижима из любой другой.

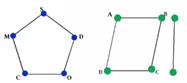
Рис. 5. Связный и несвязный граф

Граф смешанный – в котором, присутствуют и дуги и ребра.

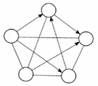
Рис. 6. Смешанный граф

Ориентированный граф - это граф, вершины которого соединены дугами.

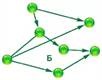
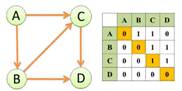
Рис. 7. Ориентированный граф

Неориентированный граф – это граф, вершины которого соединены ребрами.

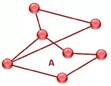
Рис 8. Неориентированный граф

Взвешенный граф- дуги или ребра имеют вес

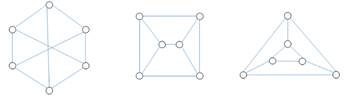
Две вершины называются смежными, если они соединены ребром (дугой).

Двудольный граф – это граф, вершины которого распадаются на два множества, где вершины одного и того же множества не соединены между собой ребрами.

Изоморфные графы –если существует взаимно-однозначное соответствие между их ребрами и вершинами, причем соответствующие ребра соединяют соответствующие вершины.

Петлей называется ребро, у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной.

Мультиграфом называется граф, в котором пара вершин соединяется несколькими различными ребрами. Для ориентированного мультиграфа вершины могут соединятся несколькими ребрами в каждом из направлений.

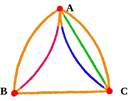
Рис. 9. Мультиграф

Псевдографом называется граф, в котором есть и петля и кратные ребра

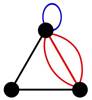
Рис. 10. Псевдограф

Маршрут графа– этопоследовательность вершин и ребер.

Маршрут называется замкнутым(циклически), если начальная и конечная вершины совпадают.

Маршрут– Простая цепь – если все вершины и ребра различны.

Пример

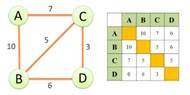
По рисунку определить: сколько вершин, ребер у графа и какова степень каждой вершины

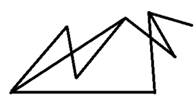
Решение

8 вершин, 9 ребер

Для определения степени вершины графа лучше все вершины обозначить буквами, а потом результаты записать в таблицу

А	Б	В	Г	Д	Е	К	Л

⇐ Предыдущая 12