Математический анализ

Математический анализ

ЛЕКЦИИ.

1. Элементы теории множеств. Числ. множества. Расширенная числ. прямая. Окрестности точек.

2. Предельные и изолированные точки. Предел функции на языке - .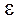

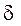Односторонние пределы. Предел последовательности.

3. Свойства функций, имеющих пределы. (единственность; ограниченность; предельный

переход в неравенстве; предел суперпозиции).

4. Теорема о сжатой функции. I - ый замечательный предел. Арифметические действия

с функциями, имеющими конечный предел. Неопределённости.

5. Б.м. и б.б. функции, их свойства. Эквивалентные. Сравнение б.м. и б.б; шкала;

порядки роста и малости; главные части.

6. Монотонные функции; существование предела. Число е. II - ой замечательный предел

и следствия из него. Таблица эквивалентных, раскрытие неопределённостей.

7. Непрерывность функции в точке. Непрерывность основных элементарных функций.

Классификация точек разрыва. Свойства функций, непрерывных на отрезке.

8. Производная. Правила дифференцирования. Таблица. Геометрический и физ. -мех. смысл у ^/.

Касательная и нормаль к графику. Связь между существованием конечной производной

и непрерывностью функции.

9. Производная сложной и обратной функции. Дифференциал; свойства; инвариантность

формы. Производные и дифференциалы высших порядков. Дифференцирование

неявной и параметрически заданной функции. Логарифмическое дифференцирование.

10. Основные теоремы дифференциального исчисления. Формула Тейлора. Правила Лопиталя.

Раскрытие неопределённостей с помощью формулы Тейлора и правил Лопиталя.

11. Локальные экстремумы. Наименьшее и наибольшее значения функции на отрезке.

Применение средств мат. анализа для исследования функции.

12. Окрестности точек в R_n_. Предел и непрерывность функции нескольких переменных (фнп).

Частные производные и их геометрический смысл. Полный и частные дифференциалы

фнп. Производная сложной фнп. Производная по направлению.

13. Производные и дифференциалы высших порядков. Теорема о смешанных производных.

Касательная плоскость и нормаль. Формула Тейлора для фнп.

14. Экстремумы фнп. Условные экстремумы. Метод множителей Лагранжа. Наименьшее

и наибольшее значения функции на замкнутом множестве.

15. Первообразная. Неопределённый интеграл и его свойства. Таблица интегралов.

Основные методы интегрирования ( замена переменной; интегрирование по частям ).

16. Интегрирование некоторых выражений, содержащих Р₂(х). Сведения о многочленах.

Разложение рациональных дробей на простейшие.

17. Интегрирование простейших дробей. Интегрирование рациональных дробей.

18. Интегрирование тригонометрических и иррациональных выражений.

19. Площадь криволинейной трапеции. Определённый интеграл. Свойства. Существование

интеграла от непрерывной функции.

20. Теорема о среднем. Формула Ньютона - Лейбница. Замена переменной.

21. Геометрические и физико-механические приложения определённых интегралов.

Понятие о методах приближённых вычислений определённых интегралов.

22. Несобственные интегралы I - го и II - го рода. Свойства. Признаки сходимости. V. P.