
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Решение задач на построение эпюр нормальных сил, нормальных напряжений, перемещений сечений бруса.
Тема: Решение задач на построение эпюр нормальных сил, нормальных напряжений, перемещений сечений бруса.
Ознакомиться с примером построения эпюр продольных сил, напряжений и перемещений.
Задача 1.Двухступенчатый стальной брус нагружен силами F1=30 кН F2=40 кН.
Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=1,5см2;А 2=2см2.
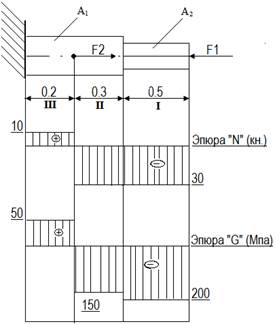
Решение.
Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.
Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
Разбиваем брус на участки.
Определяем ординаты эпюры N на участках бруса:
N1= - F1= -30кН
N2= - F2= -30кН
N3= -F1+F2= -30+40=10 кН
Строим эпюру продольных сил
Вычисляем ординаты эпюры нормальных напряжений
σ1 = 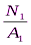 =
= 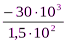 = –200МПа
= –200МПа
σ2 = 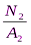 =
= 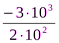 = –150МПа
= –150МПа
σ 3= 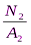 =
= 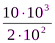 =50МПа
=50МПа
Строим эпюры нормальных напряжений.
4. Проверяем прочность бруса, если допускаемое напряжение [σ] = 160 МПа.
Выбираем максимальное по модулю расчетное напряжение. IσmaxI = 200 МПа
Подставляем в условие прочности IσmaxI ≤ [σ]
200 МПа ≤ 160 МПа. Делаем вывод, что прочность не обеспечена.
5. Определяем перемещение свободного конца бруса Е = 2∙10 5 МПа.
∆l=∆l1+∆l2+∆l3 
∆l1= 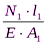 =
= 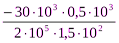 = – 0,5мм
= – 0,5мм
∆l2= 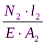 =
= 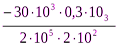 = – 0,225мм
= – 0,225мм
∆l3= 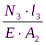 =
= 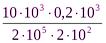 = 0,05мм
= 0,05мм
∆l= - 0,5 – 0,225 + 0,05 = – 0,675мм
Брус укоротился на 0,675мм
1. Задание: Решить задачи
Двухступенчатый стальной брус нагружен силами F1, F2.
Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=5 см2;А 2 =10 см2. Длина l = 0,5 м. Первая команда F1= 50 кН, F2 = 30 кН. Вторая команда F1= 30 кН, F2 = 50 кН.
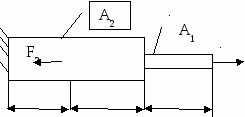
 F1
F1
l l l
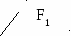

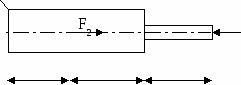
l l l
Разбить брус на участки. Пронумеровать эти участки.
Найти величину продольной силы на первом участке.
Найти величину продольной силы на втором участке.
Найти величину продольной силы на третьем участке.
Построить эпюру для продольной силы.
Найти величину нормального напряжения на первом участке.
Найти величину нормального напряжения на втором участке.
Найти величину нормального напряжения на третьем участке.
Построить эпюру для нормального напряжения.
Проверить прочность бруса. Допускаемое напряжение [σ] = 160 МПа.
Определить перемещение свободного конца бруса.
Задание 2
Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.
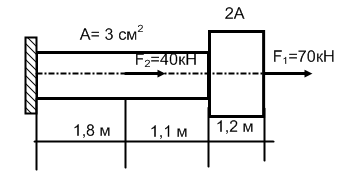
Задание 3
Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.
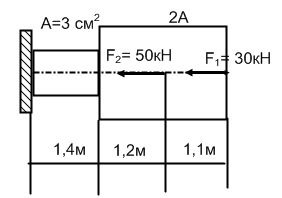
Литература
В.П. Олофинская «Техническая механика» курс лекций с вариантами практических и тестовых заданий.
Лекции по теме (конспекты).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|