Лекция. Формируемые на уроке ПК и ОК. План урока.. Ход занятия.. Актуализация темы.. Многогранники.. Призма.

Урок № 133-134

Лекция

Тема: Призма. Площадь поверхности призмы. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Площадь поверхности куба, призмы.

Цель:

Учебная:

- Дать представление о многогранниках;

Развивающая:

- формирование умений применять приемы сравнения, обобщения, выделения главного, логически излагать мысли, делать выводы, развивать речь, внимание и память.

Воспитательная:

- способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

Методы обучения: практическая работа, контрольная работа.

Оборудование: компьютер, проектор.

Тип урока: урок обобщения и систематизации знаний.

Формируемые на уроке ПК и ОК

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

План урока.

1. Организационный момент.

2. Актуализация темы.

3. Многогранники.

7. Задание на дом.

8. Подведение итогов.

Ход занятия.

1. Организационный момент –приветствие, проверка посещаемости.

2. Актуализация темы.

Обучающиеся называют трёхмерные геометрические фигуры, с которыми они знакомы.

3. Многогранники.

Призма.

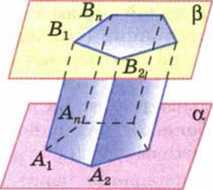Рассмотрим два равных многоугольника А₁А₂ ... А_п и В₁В₂... В_п, расположенных в параллельных плоскостях α и β так, что отрезки А₁В₁, А₂В₂, ..., А_пВ_п, соединяющие соответственные вершины многоугольников, параллельны (рис.). Каждый из п четырехугольников

А₁А₂В₂В₁, А₂А₃В₃В₂, ..., А_пА₁В₁В_п (1)

является параллелограммом, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике А₁А₂В₂В₁ стороны А₁В₁ и А₂В₂ параллельны по условию, а стороны А₁А₂ и В₁В₂ — по свойству параллельных плоскостей, пересеченных третьей плоскостью (п. 11).

Многогранник, составленный из двух равных многоугольников А₁А₂ ... А_п и В₁В₂ ... В_п, расположенных в параллельных плоскостях, и п параллело-
граммов (1), называется призмой (см. рис).

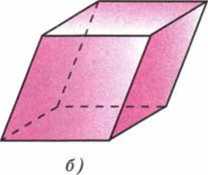
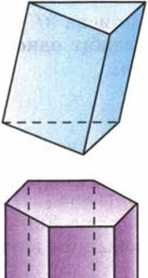Многоугольники А₁А₂ ... А_п и В₁В₂ ... В_п называются основаниями, а параллелограммы (1) – боковыми гранями призмы. Отрезки А₁В₁, А₂В₂, ..., А_пВ_пназываются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограммов (1), последовательно приложенных друг к другу, равны и параллельны. Призму с основаниями А₁А₂ ... А_пи В₁В₂ ... В_п обозначают А₁А₂ ... А_пВ₁В₂ ... В_п и называют п-угольной призмой. На рисунках изображены треугольная призма и четырехугольная призма, являющаяся па-
раллелепипедом .

Перпендикуляр, проведенный из какой-ни-
будь точки одного основания к плоскости другого осно-
вания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы — сумма площадей ее боковых граней. Площадь S_полн полной поверхности выражается через площадь S_бок боковой поверхности и площадь основания призмы формулой

S_полн = S_бок + 2S_осн

Теорема

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

12 Следующая ⇒