КРАТКАЯ ТЕОРИЯ

Лабораторная работа 5.06

определение длины световой волны при помощи колец ньютона

ЦЕЛЬ РАБОТЫ: определить длину волны падающего света на установке для наблюдения колец Ньютона.

Приборы и ПРИНАДЛЕЖНОСТИ:линза, черная плоская стеклянная пластина, светофильтры (красный, зеленый, желтый, синий), микроскоп со встроенным полупрозрачным зеркалом для получения отраженного света и измерительной шкалой в поле зрения окуляра.

Описание установки

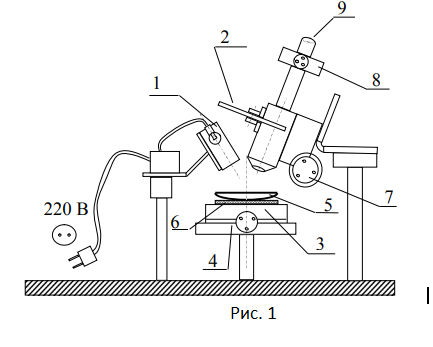
Установка (рис.1) предназначена для проведения исследований интерференции в схеме колец Ньютона и определения длины падающей волны. Источником света является лампа накаливания 1, находящаяся в осветителе. Свет от нее, проходя через светофильтр 2 и вертикальный иллюминатор микроскопа, падает на полупрозрачное зеркало 3. Отражаясь от него свет, проходит через объектив 4 и падает на плоско-выпуклую сферическую линзу 5, которая лежит на горизонтально расположенном черном стекле 6, создающем черный фон и дающем возможность четко видеть интерференционные кольца. Резкость изображения достигается с помощью винта каретки 7. Измерения радиусов (диаметров) колец Ньютона производятся по цифровой шкале 8, встроенной в окуляр 9 микроскопа. Цена деления шкалы 1×10^-3 м, радиус сферы линзы на предложенной компьютерной модели можно менять (к примеру, R = 1 м).

Источником света является лампа накаливания 1, находящаяся в осветителе. Свет от неё падает на линзу 5, которая лежит на горизонтально расположенном чёрном стекле 6, создающем тёмный фон и дающий возможность чётко видеть интерференционные кольца. Резкость изображения достигается с помощью винта 7 каретки микроскопа. Измерения радиусов колец Ньютона производятся по цифровой шкале, встроенной в окуляр 9 микроскопа и микрометрическому винту 8, при вращении которого в поле зрения микроскопа будет перемещаться крестообразный визир. Примечание: Измерение радиусов колец Ньютона можно произвести и с помощью микрометрического винта 4 предметного стола 3, передвигая с его помощью линзу, а, следовательно, и изображение в поле зрения микроскопа относительно неподвижного крестообразного визира.

КРАТКАЯ ТЕОРИЯ

Интерференцией света называется сложение нескольких когерентных световых волн, в результате которого образуется чередующиеся светлые и темные области, т.е. происходит перераспределение энергии этих волн в пространстве (вдоль фронта волны). Во всех случаях интерференции увеличение интенсивности двух волн происходит, если они приходят в данную точку в фазе, уменьшение – если в противофазе. Поэтому оптическая разность хода лучей связана с длиной волны определенными соотношениями. Разберем этот вопрос более подробно. Для этого рассмотрим тонкий прозрачный слой, изготовленный из вещества с показателем преломления n, большим, чем показатель преломления окружающей его среды (для однозначности в роли среды будет воздух). И этот слой имеет вид клина с малым углом φ (рис.2).

Рис.2

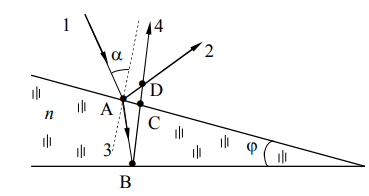Пусть на верхнюю поверхность падает под малым углом α луч 1 и в точке А разделяется на отраженный 2 и преломленный 3, который также отражается от нижней поверхности в точке В и после незначительного преломления в точке С выходит лучом 4. Лучи 2 и 4 будут когерентными, а значит будут интерферировать в точке их пересечения (точка D). Оптическая разность хода Δ этих лучей будет равна:

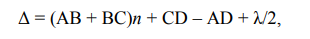(1)

слагаемое (λ/2) возникает вследствие скачка фазы на π, испытываемый волной 2 при отражении в точке А от поверхности клина с показателем преломления большим показателя преломления окружающего клин воздуха. Приближенно можно считать CD=AD=0, AB=BC=d, тогда выражение (1) для оптической разности хода примет следующий вид:

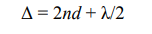(2)

Интерференционные максимумы будут наблюдаться при равенстве оптической разности хода целому числу длин волн:

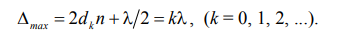(3)

Интерференционные минимумы будут наблюдаться при равенстве оптической разности хода нечетному числу полуволн:

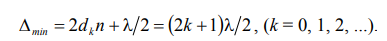(4)

В этих формулах k – порядок интерференционного максимума или минимума соответственно. Таким образом, видно, что интерференционные максимумы (минимумы) возникают при определенных значениях толщены слоя d_k , поэтому такая интерференция называется интерференцией равной толщины. Здесь речь идет о толщине слоя, а не о ширине интерференционной полосы. В случае клиновидного слоя эти максимумы и минимумы будут чередоваться в виде светлых (максимумы) и темных (минимумы) полос, параллельных ребру клина и для стороннего наблюдателя вся интерференционная картина, вследствие малости СD (рис.2) будет практически находится на поверхности клина, или вблизи этой поверхности, в то время как в других областях пространства над клином возникает лишь однородная освещенность (рис.3). Если интерференционная картина достаточно четко наблюдается вблизи какой-либо поверхности, то такая интерференция называется локализованной. Следует отметить, что отчетливость интерференционной картины уменьшается при переходе от вершины клина к её основанию. Практически полосы равной толщины можно наблюдать, поместив вблизи клина линзу и за ней экран. Роль линзы может играть хрусталик глаза, а роль экрана – сетчатка глаза

Рис.3

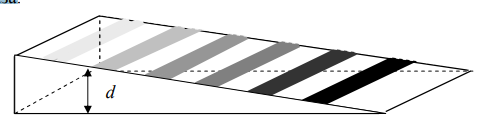
В общем случае полосы интерференционной картины на поверхности плёнки (или тонкого слоя) будут соответствовать геометрическим местам пленки, где она имеет одинаковую толщину.

При наблюдении в белом свете полосы приобретают радужную окраску. Это хорошо видно на тонких нефтяных или масляных пленках, покрывающих воду, а так же на мыльных пленках, в том числе на мыльных пузырях. Цвета побежалости на поверхностях металлов при их нагревании тоже обусловлены интерференцией на пленках прозрачных окислов. Классическим примером полос равной толщины являются кольца Ньютона, которые наблюдаются в виде концентрических колец вблизи точки соприкосновения выпуклой поверхности линзы малой кривизны с плоской поверхностью стеклянной пластины. В этом месте образуется тонкий воздушный слой (n = 1), который постепенно утолщается от точки соприкосновения к краям (рис.4,а). Если направить монохроматический световой пучок нормально к плоской поверхности линзы (луч 1), то световые волны, отраженные от верхней (луч 2) и нижней (луч 3) границ воздушной прослойки будут интерферировать между собой. В отраженном свете получится следующая картина: в точке О (рис..4) соприкосновения линзы и плоской пластины будет наблюдаться тёмная точка, окруженная серией концентрических, светлых и тёмных колец с убывающей шириной. Такая интерференция, получаемая в тонком воздушном слое, образованном между линзой и плоской стеклянной пластиной называется кольцами Ньютона, поскольку такую интерференцию впервые описал И.Ньютон в 1675 году.

Рис. 4

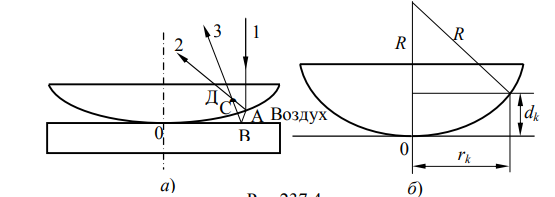
Формула (2), определяющая оптическую разность хода лучей, отраженных от двух поверхностей слоя с учётом n = 1 теперь примет вид:

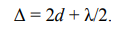(5)

Здесь также принято во внимание различия в условиях отражения от верхней и нижней поверхностей прослойки, что приводит к дополнительной разности ходе на λ/2. Эта разность возникает за счет скачка фазы на p, который происходит при отражении луча 3 от оптически более плотной среды в точке B (рис.4,а). Рассчитаем размеры (радиусы) колец Ньютона. Обозначим радиус k-го кольца (светлого или тёмного) через rk , а толщину воздушного зазора в этом месте как dk . Из рис.4,б видно, что

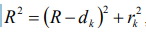
, где R – радиус кривизны линзы. Отсюда получаем радиус кольца r_k, учитывая малость d_k по сравнению с R:

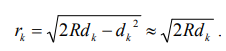(6)

Интерференционные максимумы наблюдаются при условии, что оптическая разность хода когерентных волн равна четному числу полуволн (или целому числу волн):

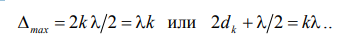(7)

Выразим из (7) значение d_k и подставим в (6), получаем радиусы светлых колец (в отраженном свете):

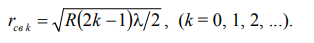(8)

Интерференционные минимумы наблюдаются при условии, что оптическая разность хода интерферирующих волн равна нечетному числу полуволн:

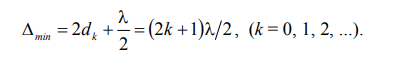(9)

Выразив значение d_k и подставив в (6), получим радиусы темных колец (в отраженном свете):

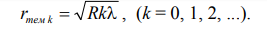(10)

Если принять k = 0, то r_k = 0, что соответствует тому, что в центре должна быть темная точка. Это действительно наблюдается в отраженном свете (рис..5,а), и обусловлено изменением фазы на π при отражении световой волны от пластины, на которой лежит линза. Кольца Ньютона наблюдаются и в проходящем свете. В этом случае проходящий луч интерферирует с лучом дважды отраженном на границе воздушной прослойки от оптически более плотной среды и каждый раз получающий скачок фазы на π и в итоге дополнительная разность хода исчезает. Поэтому в проходящем свете расположения светлых и темных колец становится обратным их расположению в отраженном свете (рис. 5,б), тогда в центре картины будет наблюдаться светлая точка. Следует отметить, что в проходящем свете интерференция наблюдается менее четко, чем в отраженном свете, так как интерферирующие волны сильно отличаются по амплитудам.

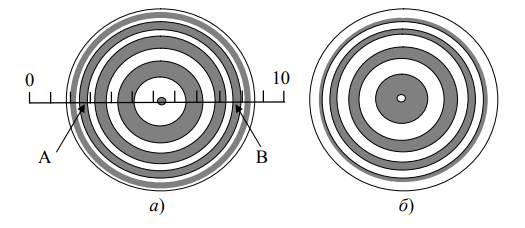
Рис. 5 Кольца Ньютона а) а отраженном свете б) в проходящем свете

Используя схему колец Ньютона можно решать следующие задачи:

1) Если известна длина волны λ, то можно измерять радиусы кривизны поверхностей линз R и осуществлять контроль правильности форм сферических и плоских поверхностей.

2) Экспериментально определяя радиус k – ого светлого кольца и радиус кривизны линзы R можно из (8) определить длину волны падающего света:

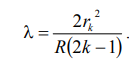(11)

Длину волны λ можно определить, также используя радиус k – ого темного кольца воспользовавшись формулой (10):

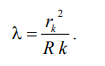(12)

Порядок выполнения работы:

1) Устанавливаем красный светофильтр. В данной виртуальной модели выбираем красный (рис.6). Указываем показатель преломления среды n=1(воздух), которая находится между линзой и пластиной, или другое значение. Радиус кривизны линзы R=1м.

2) Определяем по виртуальной модели радиусы первых двух светлых и темных колец Ньютона (К=1,2). Значения заносим в таблицу1.

3) Устанавливаем желтый светофильтр. В данной виртуальной модели выбираем желтый, зеленый, синий (рис.6). Определяем по виртуальной модели радиусы первых двух светлых и темных колец Ньютона (К=1,2). Значения заносим в таблицу 1.

4) Используя формулы (11) и (12) найти длину волны. Значения занести в таблицу1.

Светофильтр	Кольцо	Порядок интерференции К	Радиус кольца r, мм	Длина волны λ, нм	Среднее значение длины волны λ_ср, нм
Красный	светлое
	светлое
	темное
	темное
Желтый	светлое
	светлое
	темное
	темное
Зеленый	светлое
	светлое
	темное
	темное

5) Определить среднее значение длины волны. Значения занести в таблицу1.

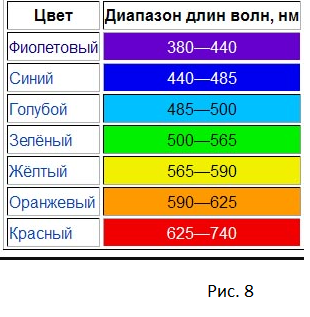
6) Сравнить результат с известными значениями длин волн (рис.8)

Контрольные вопросы

1. Сформулируйте принцип Гюйгенса.

2. Когерентные волны. Пространственная и временная когерентность. Время и длина когерентности. Оптическая разность хода (пояснить на рисуноке).

3. Явление интерференции.

4. Условия минимума и максимума интенсивности.

5. Распределение интенсивности при интерференции.

6. Интерференция на плоскопараллельной пластине. Оптическая разность хода плоскопараллельной пластине.

7. Кольца Ньютона для отраженного и проходящего света (рисунки). Радиус колец Ньютона.

8. Практическое применение явления интерференции, в частности, просветление оптики.

Литература:

1) Иродов И.Е. Волновые процессы. Основные законы: Учебное пособие для физич. спец. вузов. – 5-е изд., испр. – М.: БИНОМ. Лаборатория знаний, 2010. – 263 с. 2.

2) Савельев И.В. Курс общей физики в 4-х томах. Электричество и магнетизм. Волны. Оптика. – М.: КноРус, 2012. – Т.2. – 576 с.

3) Сивухин Д.В. Общий курс физики. Оптика – М.: ФИЗМАТЛИТ, 2005. – Т.4. – 792 с. 4.

4) Трофимова Т.И. Курс физики. – 20-е изд., стер. – М.: Изд-во «Академия», 2014. – 560 с.