Задание №1 по теме «Решение квадратных неравенств с помощью графика»

Задание №1 по теме «Решение квадратных неравенств с помощью графика»

срок выполнения 06.04- 11.04 ( 3 урока)

1.Прочитать текст параграфа 41 стр. 268 и ознакомиться с текстом ниже (разобрать решение примеров)

Графическое решение квадратных неравенств Квадратным неравенством называют неравенства вида ax2 + bx + c ˃ 0, где вместо знака ˃ может быть любой другой знак неравенства. Для решения квадратного неравенства с помощью графика нужно: – определить направление ветвей параболы по знаку старшего коэффициента квадратичной функции;

– найти корни соответствующего квадратного уравнения или установить, что их нет;

– построить эскиз графика квадратичной функции, учитывая точки пересечения (или касания) с осью Ох, если они есть;

– по графику определить промежутки, на которых функция принимает нужные значения.

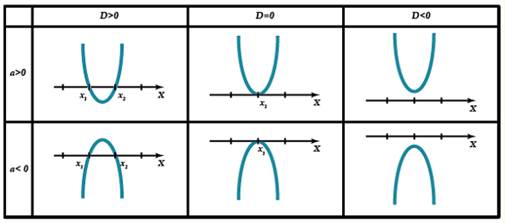
ПРИМЕР:
Решите неравенство графическим способом:
–х² + 10х –2 < 0.
РЕШЕНИЕ:
Сначала решаем квадратное уравнение:
–х² + 10х –2 = 0

D = b² – 4ac,

D = 100 – 4 × (–1) × (–21)

= 100 – 84 = 16,

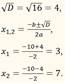
Затем схематично рисуем параболу, не высчитывая, где у нё находится вершина, ведь по сути это не нужно, у нас есть основное – точки пересечения параболы с осью Ох.

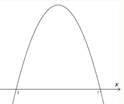
Возвращаемся к неравенству
–х² + 10х –2 < 0.
и отмечаем нужные нам промежутки:

Запишем теперь ответ.
ОТВЕТ:
х ∈ (–∞; 3) ∪ (7; +∞)
ПРИМЕР:
Решите неравенство графическим способом:
х² – 2х – 3 ˃ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х² – 2х – 3.

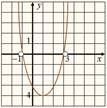
Решить неравенство
х² – 2х – 3 ˃ 0
это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны.

Замечаем, что у ˃ 0, то есть график функции расположен выше оси х, при х < –1 и при х ˃ 3. Значит, решениями неравенства служат все точки интервалов
(–∞; –1) ∪ (3; +∞).
ПРИМЕР:
Решите неравенство графическим способом:
х² – 2х – 3 < 0.

РЕШЕНИЕ:
Рассмотрим параболу
у = х² – 2х – 3.

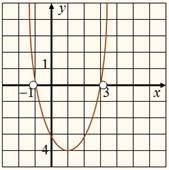
Неравенство
х² – 2х – 3 < 0
или у < 0, где
у = х² – 2х – 3,
также можно решить с помощью графика. График расположен ниже оси х, если
–1 < х < 3.
Поэтому решением данного неравенства служат все точки интервала
(–1; 3).

Алгоритм решения ( запись в тетрадь):

1. Исходное неравенство

2. Записать уравнение функции

3. Написать направление ветвей

4. Решить квадратное уравнение

5. Нарисовать схематически параболу

6. Выбрать нужный интервал с учетом знака исходного неравенства.

2. Выполнить номера по учебнику (подробное решение по алгоритму):

№ 660-664 (четные)

№ 667 (четные)

Контрольное задание : № 667 (1,3,5,7) ( выполняется на отдельном листе в тетради и фотографией присылается 10.04 по эл.почте: elenayavorskaya71@mail.ru