
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 1 № 406563. Решение.. Задание 2 № 406675. Решение.. Задание 3 № 406564. Решение.. Задание 4 № 406565. Решение.. Задание 5 № 367694. Решение.. Задание 6 № 203743. Решение.. Задание 7 № 314800. Решение.. Примечание.
1. Задание 1 № 406563
Определите, какие месяцы соответствуют указанному в таблице трафику мобильного интернета.
Заполните таблицу, в бланк ответов перенесите числа, соответствующие номерам месяцев, без пробелов, запятых и других дополнительных символов (например, для месяцев май, январь, ноябрь, август в ответе нужно записать
число 51118).
| Мобильный интернет | 2,5 Гб | 3 Гб | 3,25 Гб | 1 Гб |
| Номер месяца |
На рисунке точками показано количество минут исходящих вызовов и трафик мобильного интернета в гигабайтах, израсходованных абонентом в процессе пользования смартфоном, за каждый месяц 2019 года. Для удобства точки, соответствующие минутам и гигабайтам, соединены сплошными и пунктирными линиями соответственно.
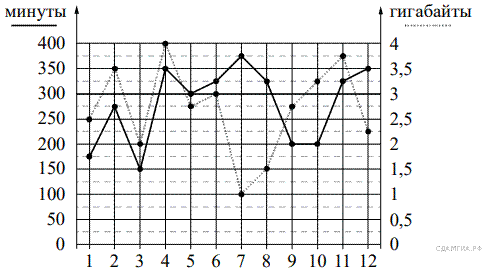
В течение года абонент пользовался тарифом «Стандартный», абонентская плата по которому составляла 350 рублей в месяц. При условии нахождения абонента на территории РФ в абонентскую плату тарифа «Стандартный» входит:
• пакет минут, включающий 300 минут исходящих вызовов на номера, зарегистрированные на территории РФ;
• пакет интернета, включающий 3 гигабайта мобильного интернета;
• пакет СМС, включающий 120 СМС в месяц;
• безлимитные бесплатные входящие вызовы.
Стоимость минут, интернета и СМС сверх пакета тарифа указана в таблице.
| Исходящие вызовы | 3 руб./мин. |
| Мобильный интернет (пакет) | 90 руб. за 0,5 Гб |
| СМС | 2 руб./шт. |
Абонент не пользовался услугами связи в роуминге. За весь год абонент отправил 110 СМС.
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года.
Из рисунка видно, что 2,5 Гб было потрачено в первый месяц, 3 Гб — потрачено в шестой, 3,25 Гб — в десятый, 1 Гб — в седьмой.
Ответ: 16107.
2. Задание 2 № 406675
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику израсходованных минут и гигабайтов.
| ПЕРИОДЫ | ХАРАКТЕРИСТИКИ | |
| А) январь−февраль Б) февраль−март В) август–сентябрь Г) ноябрь–декабрь | 1) Расход минут увеличился, а расход гигабайтов уменьшился. 2) Расход гигабайтов увеличился, а расход минут уменьшился. 3) Расход минут увеличился, и расход гигабайтов увеличился. 4) Расход минут уменьшился, и расход гигабайтов уменьшился. |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение.
Пунктирной линей на графике показан трафик мобильного интернета в гигабайтах, израсходованных за каждый месяц года, а сплошной линей — количество минут исходящих вызовов.
За период январь−февраль расход минут увеличился, и расход гигабайтов увеличился.
За период февраль−март расход минут уменьшился, и расход гигабайтов уменьшился.
За период август–сентябрь расход гигабайтов увеличился, а расход минут уменьшился.
За период ноябрь–декабрь расход минут увеличился, а расход гигабайтов уменьшился.
Таким образом, получается соответствие: А — 3, Б — 4, В — 2, Г — 1.
Ответ: 3421.
3. Задание 3 № 406564
Сколько рублей потратил абонент на услуги связи в июне?
Решение.
По рисунку видно, что за июнь абонент потратил 3 Гб интернета, 325 минут исходящих вызовов, и в условии сказано, что за год отправил 110 СМС.
Количество потраченного интернета и СМС не превысило это количество в пакете тарифа, а исходящих вызовов сверх пакета было потрачено 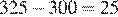 минут.
минут.
Вычислим стоимость услуг связи, потраченных абонентом в июне:
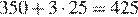 рублей.
рублей.
Ответ: 425.
4. Задание 4 № 406565
Какое наименьшее количество минут исходящих вызовов за месяц было в 2019 году?
Решение.
Сплошной линей на графике показано количество минут исходящих вызовов, израсходованных за каждый месяц года.
Из рисунка видно, что в третьем месяце было потрачено 150 минут, что является наименьшим количеством за 2019 год.
Ответ: 150.
5. Задание 5 № 367694
Компания выбирает место для строительства торгово‐развлекательного комплекса: на месте квартала старых одноэтажных домов в центре города или на окраине города. Стоимость прокладки 1 метра коммуникаций равна 6000 рублей. В аренду планируется сдавать 4000 м2 площади комплекса. Стоимость земли, цена строительства комплекса с учётом сноса старых зданий и предполагаемая стоимость сдачи даны в таблице.
| Место | Цена земли (млн руб.) | Цена строительства (млн руб.) | Длина коммуникаций (м) | Стоимость аренды за 1 м2 (руб./месяц) |
| Центр | 64,4 | |||
| Окраина | 11,2 |
Обдумав оба варианта, компания выбрала местом для строительства центр города. Через сколько месяцев после начала сдачи в аренду торговых площадей построенного комплекса более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций? Ответ округлите до целых.
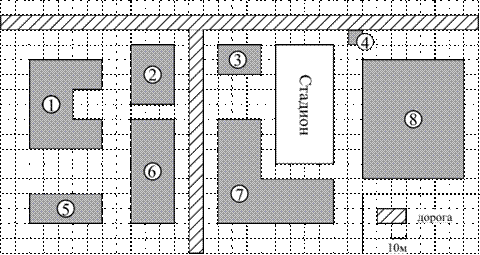
На плане (см. рисунок) изображён район города, в котором живёт Петя. Сторона каждой клетки на плане равна 10 м.
Дом, в котором живёт Петя, обозначен цифрой 6. Прямо напротив дома, где живёт Петя, через дорогу находится дом в форме буквы «Г», где живёт его друг Вася. Рядом с домом, где живёт Петя, расположен дом, где живёт одноклассница Таня, а напротив него через дорогу имеется здание банка площадью 600 м2. А с другой стороны дома, где живёт Таня, расположен детский сад. Недалеко от детского сада и дома, где живёт Петя, находится магазин. Также имеется автобусная остановка, обозначенная цифрой 4, а в десяти метрах от неё — квартал старых одноэтажных домов.
Решение.
Стоимость постройки ТРК в центре города равна
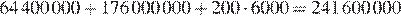 рублей.
рублей.
Стоимость постройки ТРК на окраине города равна
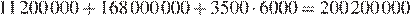 рублей.
рублей.
Разница в стоимости составляет
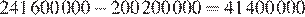 рублей.
рублей.
Разница в стоимости аренды составляет
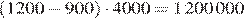 рублей.
рублей.
Значит, более высокая стоимость аренды компенсирует разность в стоимости земли, строительства и прокладывания коммуникаций через 34,5 месяцев. Округляя, получаем ответ — 35 месяцев.
Ответ: 35.
6. Задание 6 № 203743
Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
1) 
| 2) 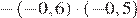
| 3) 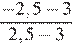
| 4) 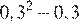
|
Решение.
Найдём значения выражений:
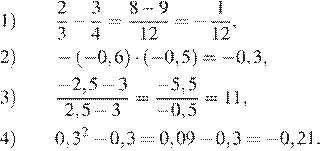
Таким образом, искомое выражение указано под номером 3.
7. Задание 7 № 314800
На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?
В ответе укажите номер правильного варианта.

1) 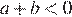
2) 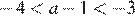
3) 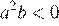
4) 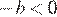
Решение.
Заметим, что 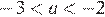 и
и 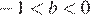 , и проверим все варианты ответа:
, и проверим все варианты ответа:
1) 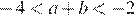 , значит,
, значит, 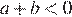 — верно.
— верно.
2) 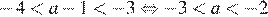 — верно.
— верно.
3) 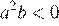 — верно, поскольку
— верно, поскольку 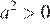 , а
, а 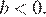
4) 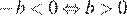 — неверно.
— неверно.
Неверным является утверждение 4.
Примечание.
Нетрудно заметить, что справедливо неравенство: 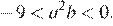
8. Задание 8 № 341704
Найдите значение выражения 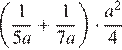 при a = 7,7.
при a = 7,7.
Решение.
Упростим выражение:
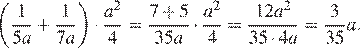
Подставим в полученное выражение значение 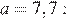
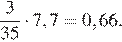
Ответ: 0,66.
9. Задание 9 № 338610
Решите уравнение 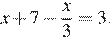
Решение.
Последовательно получаем:
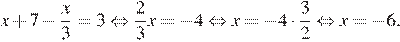
Ответ: −6.
10. Задание 10 № 325541
Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Решение.
Вероятность того, что стрелок промахнётся равна 1 − 0,8 = 0,2. Вероятность того, что стрелок первые два раза попал по мишеням равна 0,82 = 0,64. Откуда, вероятность события, при котором стрелок сначала два раза попадает в мишени, а третий раз промахивается равна 0,64 · 0,2 = 0,128.
Ответ: 0,128.
11. Задание 11 № 193089
Найдите значение  по графику функции
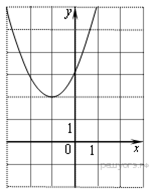
по графику функции 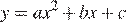 , изображенному на рисунке.
, изображенному на рисунке.
1) 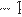
| 2) 
| 3) 
| 4) 
|
Решение.
Абсцисса вершины параболы равна −1, поэтому 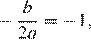 откуда
откуда 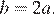 Парабола пересекает ось ординат в точке с ординатой 3, поэтому
Парабола пересекает ось ординат в точке с ординатой 3, поэтому 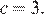 Тем самым, уравнение параболы принимает вид
Тем самым, уравнение параболы принимает вид 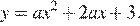 Поскольку парабола проходит через точку (−1; 2), имеем:
Поскольку парабола проходит через точку (−1; 2), имеем:
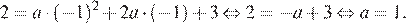
Верный ответ указан под номером 2.
Ответ: 2.
12. Задание 12 № 338396
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
Решение.
Найдем расстояние, на котором находится наблюдатель от места удара молнии:
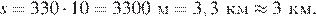
Ответ: 3.
13. Задание 13 № 311312
Решите неравенство 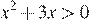 .
.
В ответе укажите номер правильного варианта.
1) 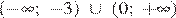
2) 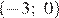
3) 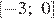
4) 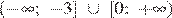
Решение.
Решим данное неравенство:
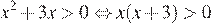 . Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.
. Произведение двух сомножителей будет больше нуля, если его сомножители имеют одинаковый знак.
В данном случае это выполняется при следующих значениях  :
:
1) 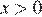 ;
;
2) 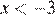 ;
;
Решением неравенства будет являться объединение этих промежутков: 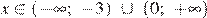 , что соответствует первому варианту ответа.
, что соответствует первому варианту ответа.
Ответ: 1
14. Задание 14 № 394426
Давление воздуха под колоколом равно 625 мм ртутного столба. Каждую минуту насос откачивает из-под колокола 20% находящегося там воздуха. Определите давление (в мм рт. ст.) через 5 минут после начала работы насоса.
Решение.
Через минуту давление воздуха (в мм рт. ст.) под колоколом станет 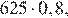 через две минуты —
через две минуты — 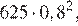 ..., через 5 минут давление станет
..., через 5 минут давление станет 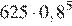 или
или
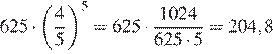 мм рт. ст.
мм рт. ст.
Ответ: 204,8.
15. Задание 15 № 348371

Высота BH ромба ABCD делит его сторону AD на отрезки AH = 44 и HD = 11. Найдите площадь ромба.
Решение.
Заметим, что сторона ромба AB = AD = AH + HD = 44 + 11 = 55.
Из прямоугольного треугольника ABH найдем BH по теореме Пифагора:
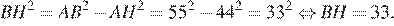
Площадь ромба можно найти как произведение основания на высоту:
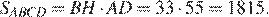
Ответ: 1815.
16. Задание 16 № 339975

Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение.
Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника 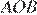 по теореме Пифагора найдём
по теореме Пифагора найдём 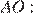
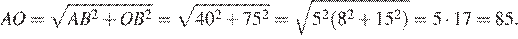
Найдём 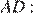
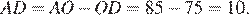
Ответ: 10.
17. Задание 17 № 324017
 Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Решение.
 Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что
Проведём построение и введём обозначения, как показано на рисунке. Учитывая, что 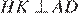 и
и 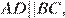 получаем
получаем 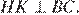 Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники
Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники 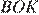 и
и 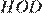 , они прямоугольные,
, они прямоугольные, 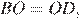
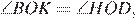 следовательно, треугольники
следовательно, треугольники 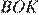 и
и 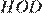 равны, откуда
равны, откуда  то есть высота
то есть высота 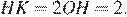 Найдём площадь ромба как произведение стороны на высоту:
Найдём площадь ромба как произведение стороны на высоту:
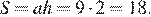
Ответ: 18.
18. Задание 18 № 311485

На квадратной сетке изображён угол 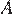 . Найдите
. Найдите 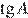 .
.
Решение.
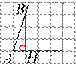
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,
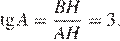
Ответ: 3.
19. Задание 19 № 341676
Какие из следующих утверждений верны?
1) Треугольника со сторонами 1, 2, 4 не существует.
2) Смежные углы равны.
3) Все диаметры окружности равны между собой.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
1) «Треугольника со сторонами 1, 2, 4 не существует» — верно, большая сторона треугольника должна быть меньше суммы двух других.
2) «Смежные углы равны» — неверно, смежные углы 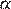 и
и 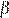 связаны соотношением:
связаны соотношением: 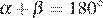 .
.
3) «Все диаметры окружности равны между собой» — верно.
Ответ: 13.
20. Задание 20 № 311591
Решите уравнение: 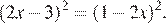
Решение.
Перенесем все члены влево и применим формулу разности квадратов:
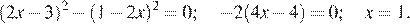
Другой способ. Раскроем скобки, пользуясь формулой квадрата разности:
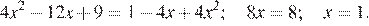
Ответ: 1.
21. Задание 21 № 314507
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
Решение.
Пусть скорость пешехода — x км/ч, 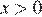 , тогда скорость велосипедиста равна (x + 11) км/ч.
, тогда скорость велосипедиста равна (x + 11) км/ч.
Составим таблицу по данным задачи:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| Пешеход | 
| 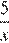
| |
| Велосипедист | 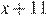
| 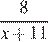
|
Так как по пути велосипедист сделал остановку на  ч., составим уравнение:
ч., составим уравнение:
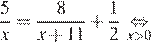
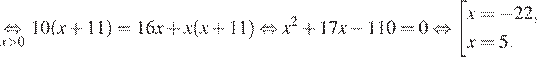
Корень −22 не подходит нам по условию задачи. Скорость пешехода равна 5 км/ч.
Ответ: 5 км/ч.
22. Задание 22 № 353274
Постройте график функции 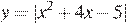 . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение.
График данной функции — это график параболы 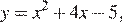 отрицательная часть которого отражена относительно оси
отрицательная часть которого отражена относительно оси 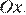 Этот график изображён на рисунке:
Этот график изображён на рисунке:
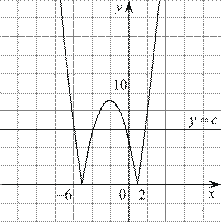
Прямая, параллельная оси абсцисс задаётся формулой 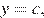 где
где  — постоянная. Из графика видно, что прямая
— постоянная. Из графика видно, что прямая  может иметь с графиком функции не более четырёх общих точек.
может иметь с графиком функции не более четырёх общих точек.
Ответ: 4.
23. Задание 23 № 333321
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 .
Решение.
 Углы
Углы 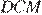 и
и 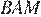 равны как накрест лежащие, углы
равны как накрест лежащие, углы 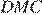 и
и 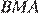 равны как вертикальные, следовательно, треугольники
равны как вертикальные, следовательно, треугольники 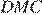 и
и 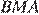 подобны по двум углам.
подобны по двум углам.
Значит, 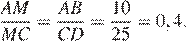 Следовательно,
Следовательно,
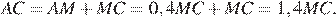
Откуда 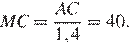
Ответ: 40.
24. Задание 24 № 349626
Окружности с центрами в точках 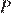 и
и 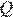 не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a:b. Докажите, что диаметры этих окружностей относятся как a:b.
Решение.

Проведём построения и введём обозначения, как показано на рисунке. Пусть 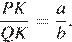 Рассмотрим треугольники
Рассмотрим треугольники 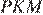 и
и 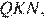 они прямоугольные, углы
они прямоугольные, углы 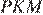 и
и 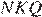 равны как вертикальные, следовательно, треугольники подобны, откуда
равны как вертикальные, следовательно, треугольники подобны, откуда 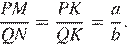 Отношение радиусов равно отношению диаметров.
Отношение радиусов равно отношению диаметров.
25. Задание 25 № 311708
В прямоугольном треугольнике ABC с прямым углом B, проведена биссектриса угла A. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне BC в точке K. Найдите угол BCK, если известно, что угол ACB равен 40°.
Решение.

Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда 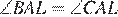 как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса
как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса 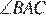 . Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой
. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой 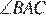 . Заметим, что
. Заметим, что 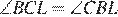 как вписанные углы, опирающиеся на равные дуги.
как вписанные углы, опирающиеся на равные дуги.
Пусть 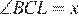 . Четырехугольник ACLB — вписанный, поэтому
. Четырехугольник ACLB — вписанный, поэтому 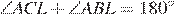 , то есть
, то есть 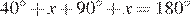 , откуда
, откуда 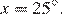 Так как точки K и L совпадают,
Так как точки K и L совпадают, 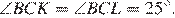
Ответ: 25°.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|