
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Задание 12 № 311920. Решение.. Задание 13 № 352671. Решение.. Задание 14 № 394424. Решение.. Примечание.
Решение.
Если прямая задана уравнением 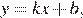 то при
то при 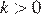 функция возрастает, при
функция возрастает, при 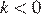 — убывает. Значению
— убывает. Значению 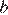 соответсвует значение функции в точке
соответсвует значение функции в точке 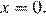 Таким образом, графику A соответствуют коэфициенты 2, Б − 1, В − 4.
Таким образом, графику A соответствуют коэфициенты 2, Б − 1, В − 4.
Ответ: 214.
12. Задание 12 № 311920
Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле 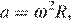 где
где 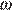 — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
— угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.
Решение.
Выразим радиус окружности: 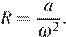 Подставим значения переменных
Подставим значения переменных 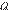 и
и 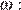
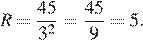
Ответ: 5.
13. Задание 13 № 352671
На каком рисунке изображено множество решений неравенства 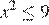 ?
?
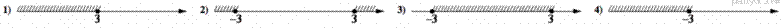
Решение.
Решим неравенство:
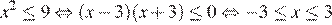
Ответ: 3.
14. Задание 14 № 394424
Служившему воину дано вознаграждение: за первую рану 1 копейка, за другую — 2 копейки, за третью — 4 копейки и т. д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран.
Решение.
Количество ран составляет геометрическую прогрессию с первым членом  вторым членом
вторым членом  а значит, знаменатель геометрической прогрессии
а значит, знаменатель геометрической прогрессии  Найдем сумму членов геометрической прогрессии:
Найдем сумму членов геометрической прогрессии:
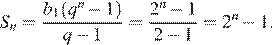
По условию, эта сумма равна 65 535. Чтобы узнать количество ран, необходимо найти количество членов прогрессии n:
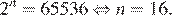
Ответ: 16.
Примечание.
Это задание взято из учебника математики 1795 года «Полный курс чистой математики, сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (цит. по Я. И . Перельман «Занимательная алгебра»).
15. Задание 15 № 323937
 Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.
Решение.
Пусть a сторона ромба, h — его высота. Все стороны ромба равны, поэтому 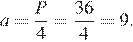 Площадь ромба можно найти как произведение стороны на высоту:
Площадь ромба можно найти как произведение стороны на высоту:
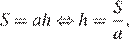
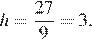
Ответ: 3.
16. Задание 16 № 350606
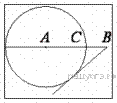
На отрезке 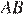 выбрана точка
выбрана точка 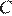 так, что
так, что  и
и  . Построена окружность с центром
. Построена окружность с центром 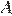 , проходящая через
, проходящая через 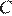 . Найдите длину отрезка касательной, проведённой из точки
. Найдите длину отрезка касательной, проведённой из точки 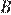 к этой окружности.
к этой окружности.
Решение.
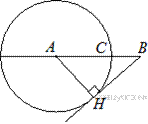 Проведём радиус
Проведём радиус 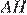 в точку касания. Из прямоугольного треугольника
в точку касания. Из прямоугольного треугольника 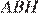 по теореме Пифагора найдём
по теореме Пифагора найдём 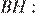
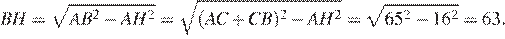
Ответ: 63.
17. Задание 17 № 324117
 Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Решение.
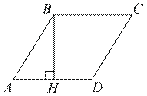 Проведём высоту в ромбе и введём обозначения, как показано на рисунке. Все стороны ромба равны, поэтому
Проведём высоту в ромбе и введём обозначения, как показано на рисунке. Все стороны ромба равны, поэтому 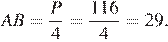 Найдём
Найдём 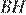 из прямоугольного треугольника
из прямоугольного треугольника 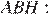
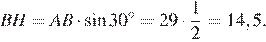
Найдём площадь ромба как произведение стороны на высоту:
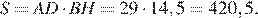
Ответ: 420,5.
18. Задание 18 № 349071

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
Решение.
Посчитаем количество клеток внутри закрашенной области: их 10.
Ответ: 10.
19. Задание 19 № 401818
Какие из следующих утверждений верны?
1) Все высоты равностороннего треугольника равны.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) В любой ромб можно вписать окружность.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Все высоты равностороннего треугольника равны» — верно, так как в равностороннем треугольнике все высоты равны между собой.
2) «Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу» — неверно, так как угол, вписанный в окружность, равен половине соответствующего центрального угла, опирающегося на ту же дугу.
3) «В любой ромб можно вписать окружность» — верно, так как суммы противоположных сторон ромба равны.
Ответ: 13.
20. Задание 20 № 341340
Решите систему уравнений 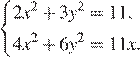
Решение.
Преобразуем систему уравнений:
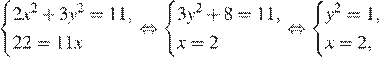
откуда получаем решения системы уравнений : (2; −1) и (2; 1).
Ответ: (2; −1); (2; 1).
21. Задание 21 № 352780
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 33 минуты раньше, чем велосипедист приехал в А, а встретились они через 22 минуты после выезда. Сколько часов затратил на путь из В в А велосипедист?
Решение.
Пусть 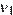 — скорость мотоциклиста,
— скорость мотоциклиста, 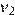 — скорость велосипедиста. Примем расстояние между городами за единицу. Мотоциклист и велосипедист встретились через 22 минуты, то есть через
— скорость велосипедиста. Примем расстояние между городами за единицу. Мотоциклист и велосипедист встретились через 22 минуты, то есть через  часа, после выезда, поэтому
часа, после выезда, поэтому 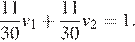 Мотоциклист прибыл в B на 33 минуты раньше, чем велосипедист в А, откуда
Мотоциклист прибыл в B на 33 минуты раньше, чем велосипедист в А, откуда 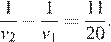 Получаем систему уравнений:
Получаем систему уравнений:
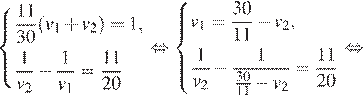
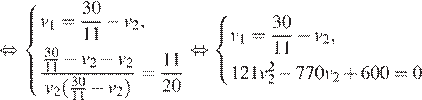
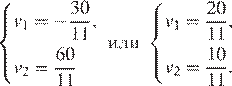
Скорость мотоциклиста не может быть отрицательной, поэтому скорость велосипедиста равна 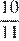 , а время, затраченное на весь путь равно
, а время, затраченное на весь путь равно 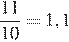
Ответ: 1,1.
22. Задание 22 № 314804
Постройте график функции 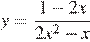 и определите, при каких значениях
и определите, при каких значениях 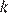 прямая
прямая 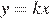 имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение для функции:
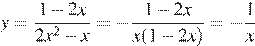 (при
(при 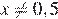 ).
).
Таким образом, получили, что график нашей функции сводится к графику функции 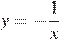 с выколотой точкой
с выколотой точкой 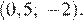
Построим график функции (см. рисунок).

Заметим, что прямая 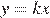 проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку
проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку 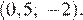 Подставим координаты этой точки в уравнение прямой и найдём коэффициент
Подставим координаты этой точки в уравнение прямой и найдём коэффициент 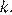
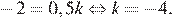
Ответ: −4.
23. Задание 23 № 339487
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 18, а сторона BC в 1,2 раза меньше стороны AB.
Решение.
 Поскольку четырёхугольник
Поскольку четырёхугольник 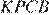 вписан в окружность, сумма противоположных углов равна 180°, следовательно,
вписан в окружность, сумма противоположных углов равна 180°, следовательно, 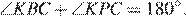 Углы
Углы 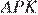 и
и 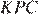 — смежные, следовательно,
— смежные, следовательно, 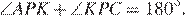 Из приведённых равенств, получаем, что
Из приведённых равенств, получаем, что 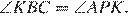 Рассмотрим треугольники
Рассмотрим треугольники 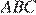 и
и 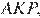 угол
угол 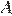 — общий, углы
— общий, углы 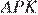 и
и 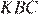 равны, следовательно, треугольники подобны, откуда
равны, следовательно, треугольники подобны, откуда 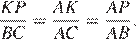 Используя равенство
Используя равенство 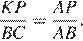 найдём
найдём 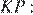
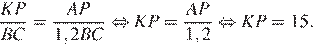
Ответ: 15.
24. Задание 24 № 352846
Окружности с центрами в точках 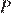 и
и 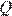 пересекаются в точках
пересекаются в точках 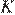 и
и 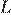 , причём точки
, причём точки 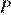 и
и 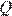 лежат по одну сторону от прямой
лежат по одну сторону от прямой 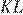 . Докажите, что прямые
. Докажите, что прямые 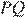 и
и 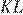 перпендикулярны.
перпендикулярны.
Решение.

Проведём медиану QM. Стороны KQ и LQ равны как радиусы окружности, поэтому треугольник KLQ — равнобедренный, следовательно, медиана QM является также высотой. Проведём медиану PM. Стороны KP и LP равны как радиусы окружности, поэтому треугольник KLP — равнобедренный, следовательно, медиана PM является также высотой. Прямые QM и PM перпендикулярны одной и той же прямой KL, следовательно, они параллельны. Эти прямые проходят через одну и ту же точку M, значит, они совпадают. Таким образом прямая KL перпендикулярна прямой PQ.
25. Задание 25 № 340054
В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Решение.
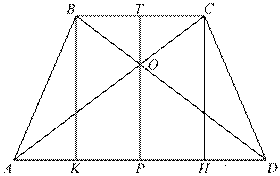 Проведём построения и введём обозначения, как показано на рисунке. В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны:
Проведём построения и введём обозначения, как показано на рисунке. В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны:
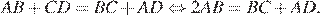
Периметр трапеции — сумма длин всех сторон:
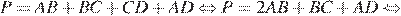
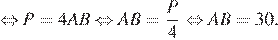
Следовательно, 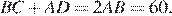 Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
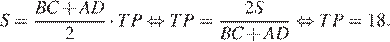
Высоты 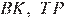 и
и 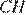 равны. Из прямоугольного треугольника
равны. Из прямоугольного треугольника 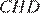 найдём
найдём 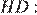
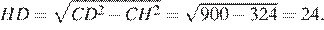
Рассмотрим треугольники 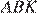 и
и 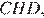 они прямоугольные,
они прямоугольные, 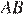 равно
равно 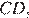
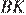 равно
равно 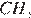 следовательно, треугольники равны, откуда
следовательно, треугольники равны, откуда 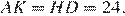 Прямые
Прямые 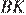 и
и 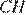 перпендикулярны прямой
перпендикулярны прямой 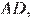 поэтому они параллельны,
поэтому они параллельны, 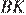 равно
равно 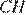 , следовательно, четырёхугольник
, следовательно, четырёхугольник 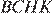 — параллелограмм, по признаку параллелограмма, откуда
— параллелограмм, по признаку параллелограмма, откуда 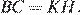 Рассмотрим выражение для отрезка
Рассмотрим выражение для отрезка 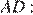
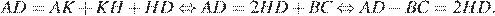
Получаем систему уравнений на отрезки 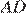 и
и 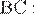
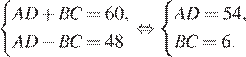
Рассмотрим треугольники 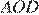 и
и 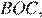 углы CAD и BCA равны как накрест лежащие при параллельных прямых, углы
углы CAD и BCA равны как накрест лежащие при параллельных прямых, углы 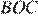 и
и 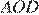 равны как вертикальные, следовательно, треугольники подобны. Откуда:
равны как вертикальные, следовательно, треугольники подобны. Откуда:
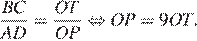
Высота 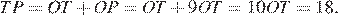 Значит, искомое расстояние
Значит, искомое расстояние 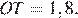
Ответ: 1,8.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|