
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тригонометрические функции числового аргумента (определение, значения, знаки, чётность, нечётность, периодичность, основные тождества).
Тригонометрические функции числового аргумента (определение, значения, знаки, чётность, нечётность, периодичность, основные тождества).
Формулы приведения.
В прямоугольном треугольнике Для произвольного угла
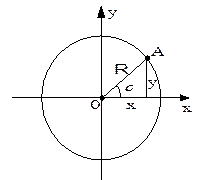
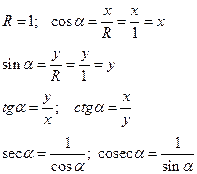
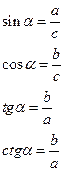

Основные тригонометрические тождества
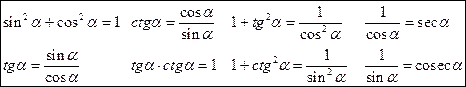
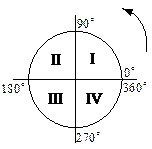
Золотые углы
| |||||||||||||||||||||||||||||||||||||||||||||||||
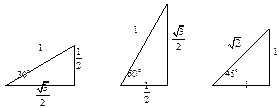 | |||||||||||||||||||||||||||||||||||||||||||||||||

| Знаки функций по четвертям | ||||
| I | II | III | IV | |
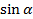
| + | + | - | - |
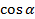
| + | - | - | + |
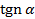
| + | - | + | - |
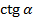
| + | - | + | - |
Углы 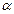 и
и 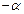
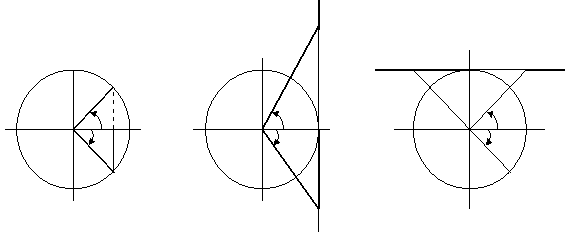
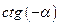 | ||||||||||||||||||||||||
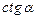 | ||||||||||||||||||||||||
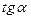 | ||||||||||||||||||||||||
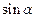 | ||||||||||||||||||||||||
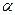 | 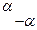 | 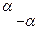 | ||||||||||||||||||||||
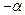 | ||||||||||||||||||||||||
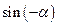 | ||||||||||||||||||||||||
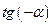 | ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
 |
Периодичность:
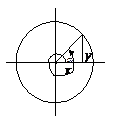
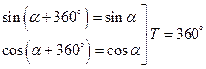 – период
– период
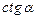
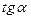
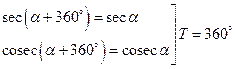 – период
– период
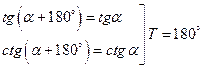 – период
– период
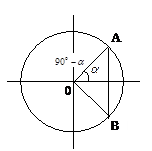 Формулы приведения:
Формулы приведения:
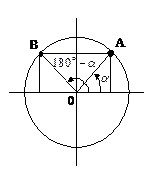
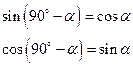
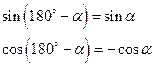
1) Знак результата берется по знаку данной функции в зависимости от четверти.
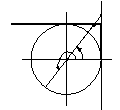
2) Если острый угол берется при горизонтальном диаметре, т.е. 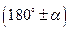 и
и 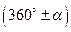 , то название функции не изменяется; если при вертикальном, т.е.
, то название функции не изменяется; если при вертикальном, т.е. 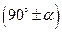 и
и 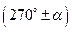 , то название функции изменяется на сходную.
, то название функции изменяется на сходную.
Примеры:
1.Найдите значения других трех тригонометрических функций, если 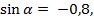
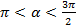 ;
;
Решение:
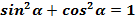 (1)
(1)
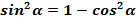 (2)
(2)
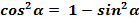 (3)
(3)
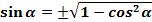 (4)
(4)
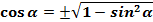 (5)
(5)
Найдем косинус угла 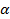 . Воспользуемся формулой (5)
. Воспользуемся формулой (5)
Угол 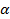 лежит в третьей четверти, значит имеет знак « минус»
лежит в третьей четверти, значит имеет знак « минус»
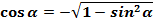 =
= 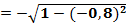 =
= 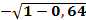 =
= 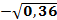 = - 0,6
= - 0,6
Нам известно, что tg 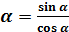 ; ctg
; ctg 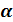 =
= 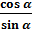
Следовательно, tg 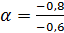 =
=  ; ctg
; ctg 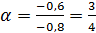
Ответ:
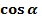 = - 0,6; tg
= - 0,6; tg 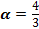 ; ctg
; ctg 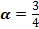
Задание №1 (на дом)
Найдите значения других трех тригонометрических функций, если 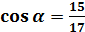 ,
,
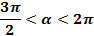
Задание №2 (на дом)
1. Найдите tg 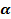 , если
, если 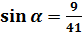 и
и 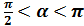
Пример 2. Используя формулы приведения, найти значение выражения .
Решение:
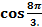 =
= 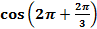 =
= 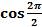 =
= 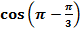 =
= 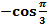 = -
= - 
Задание №3 (на дом)
Найдите значение выражения 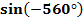
Задание №4 (на дом)
Используя формулы приведения, упростить выражение:
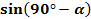 +
+ 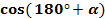 +tg
+tg 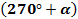 +ctg
+ctg 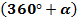
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
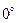
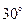
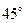
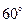
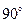
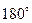
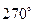
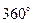
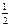
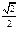
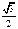
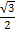
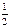
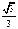
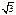
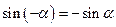 (нечётная)
(нечётная)
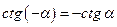 (нечётная)
(нечётная)
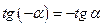 (нечётная)
(нечётная)