ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13. Краткие теоретические сведения. Образец выполнения заданий

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 13

Тема: Решение простейших задач на определение вероятности с использованием теоремы сложения и умножения вероятностей.

Краткие теоретические сведения

Теорема сложения вероятностей. Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:

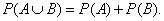
Сумма вероятностей противоположных событий также равна 1:

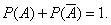
Теорема умножения вероятностей для независимых событий. Вероятность одновременного наступления двух независимых событий А и В 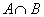равна произведению вероятностей этих событий и вычисляется по формуле:

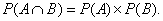
Образец выполнения заданий

Задача 1. Магазин получил продукцию в ящиках с четырех оптовых складов: четыре с 1-го, пять со 2-го, семь с 3-го и четыре с 4-го. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада.

Решение:всего получено магазином: 4 + 5 + 7 + 4 = 20 ящиков.

По классическому определению:
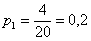– вероятность того, что для продажи будет выбран ящик с 1-го склада;
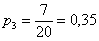– вероятность того, что для продажи будет выбран ящик с 3-го склада.

По теореме сложения несовместных событий:
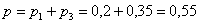– вероятность того, что для продажи будет выбран ящик с первого или третьего склада.

Ответ: 0,55

Задача 2. В каждом из трех ящиков имеется по 10 деталей. В первом ящике 8 стандартных деталей, во втором – 7, в третьем – 9. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.

Решение: вероятность извлечения стандартной или нестандартной детали из любого ящика не зависит от того, какие детали будут извлечены из других ящиков, поэтому в задаче речь идёт о независимых событиях. Рассмотрим следующие независимые события:

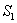– из 1-го ящика извлечена стандартная деталь;
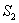– из 2-го ящика извлечена стандартная деталь;
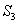– из 3-го ящика извлечена стандартная деталь.

По классическому определению:
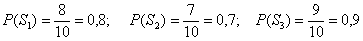– соответствующие вероятности.

Интересующее нас событие (из 1-го ящика будет извлечена стандартная деталь и из 2-го стандартная и из 3-го стандартная) выражается произведением .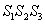

По теореме умножения вероятностей независимых событий:

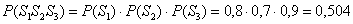– вероятность того, что из трёх ящиков будет извлечено по одной стандартной детали.

Ответ: 0,504

Задача 3. В коробке 10 красных и 6 синих пуговиц. Наудачу извлекаются две пуговицы. Какова вероятность того, что они будут одноцветными?

Решение:всего: 10 + 6 = 16 пуговиц в коробке
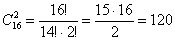способами можно извлечь 2 пуговицы из коробки;
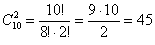способами можно извлечь 2 красные пуговицы;
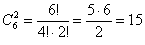способами можно извлечь 2 синие пуговицы.
По классическому определению:
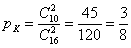– вероятность того, что из коробки будут извлечены две красные пуговицы;
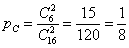– вероятность того, что из коробки будут извлечены две синие пуговицы.
По теореме сложения вероятностей несовместных событий:
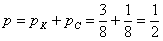– вероятность того, что из коробки будут извлечены две одноцветные пуговицы.
Ответ: 0,5

Содержание работы

Вариант 1.

Задача 1. Магазин получил продукцию в ящиках с трех оптовых складов: пять с 1-го, три со 2-го и шесть с 3-го. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада. (Ответ округлите до сотых)

Задача 2. В каждом из трех ящиков имеется по 12 деталей. В первом ящике 3 стандартных деталей, во втором – 6, в третьем – 9. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.

Задача 3. В коробке 8 красных и 4 синих пуговиц. Наудачу извлекаются две пуговицы. Какова вероятность того, что они будут одноцветными?

Вариант 2.

Задача 1. Магазин получил продукцию в ящиках с трех оптовых складов: восемь с 1-го, семь со 2-го и четыре с 3-го. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада. (Ответ округлите до сотых)

Задача 2. В каждом из трех ящиков имеется по 16 деталей. В первом ящике 8 стандартных деталей, во втором – 4, в третьем – 12. Из каждого ящика наудачу извлекают по одной детали. Найти вероятность того, что все детали окажутся стандартными.

Задача 3. В коробке 6 красных и 5 синих пуговиц. Наудачу извлекаются две пуговицы. Какова вероятность того, что они будут одноцветными?