
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производная сложной функции. Примеры решений
Производная сложной функции. Примеры решений
Смотрим на правило дифференцирования сложной функции:
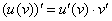
Разбираемся. Прежде всего, обратим внимание на запись 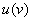 . Здесь у нас две функции –
. Здесь у нас две функции – 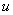 и
и 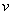 , причем функция
, причем функция 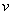 , образно говоря, вложена в функцию
, образно говоря, вложена в функцию 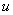 . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию 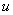 я буду называть внешней функцией, а функцию
я буду называть внешней функцией, а функцию 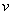 – внутренней (или вложенной) функцией.
– внутренней (или вложенной) функцией.
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции 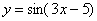
Под синусом у нас находится не просто буква «икс», а целое выражение 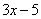 , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
, поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
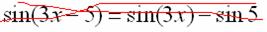
В данном примере уже из моих объяснений интуитивно понятно, что функция 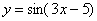 – это сложная функция, причем многочлен
– это сложная функция, причем многочлен 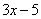 является внутренней функцией (вложением), а
является внутренней функцией (вложением), а 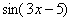 – внешней функцией.
– внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде 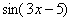 понятно, что под синус вложен многочлен
понятно, что под синус вложен многочлен 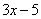 . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения 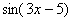 при
при 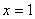 (вместо единицы может быть любое число).
(вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: 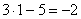 , поэтому многочлен
, поэтому многочлен 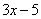 и будет внутренней функцией
и будет внутренней функцией 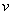 :
:
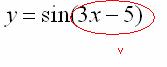
Во вторую очередь нужно будет найти 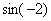 , поэтому синус – будет внешней функцией:
, поэтому синус – будет внешней функцией:
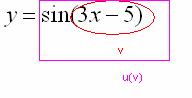
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции 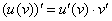 .
.
Начинаем решать.
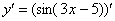
Сначала находим производную внешней функции 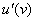 (синуса), смотрим на таблицу производных элементарных функций и замечаем, что
(синуса), смотрим на таблицу производных элементарных функций и замечаем, что 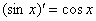 . Все табличные шаблоны применимы и в том случае, если «икс» заменить любой дифференцируемой функцией
. Все табличные шаблоны применимы и в том случае, если «икс» заменить любой дифференцируемой функцией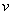 . В данном примере ВМЕСТО «икс» у нас
. В данном примере ВМЕСТО «икс» у нас 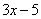 :
:
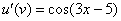
Обратите внимание, что внутренняя функция 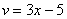 не изменилась, её мы не трогаем.
не изменилась, её мы не трогаем.
Ну и совершенно очевидно, что 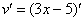
Результат применения формулы 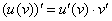 в чистовом оформлении выглядит так:
в чистовом оформлении выглядит так:
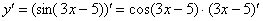
Далее мы берем производную внутренней функции, она очень простая:
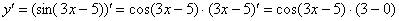
Постоянный множитель обычно выносят в начало выражения:
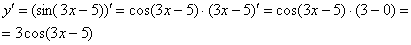
Готово
Пример 2
Найти производную функции 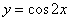
Это пример для самостоятельного решения (ответ в конце урока).
Пример 3
Найти производную функции 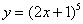
Как всегда записываем:
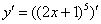
Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения 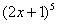 при
при 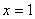 . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:
. Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: 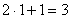 , значит, многочлен
, значит, многочлен 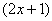 – и есть внутренняя функция:
– и есть внутренняя функция:
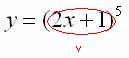
И, только потом выполняется возведение в степень 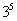 , следовательно, степенная функция – это внешняя функция:
, следовательно, степенная функция – это внешняя функция:
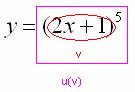
Согласно формуле 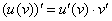 , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу:
, сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: 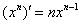 . Повторяем еще раз: любой табличный шаблон справедлив не только для «икс», но и для любой дифференцируемой функции
. Повторяем еще раз: любой табличный шаблон справедлив не только для «икс», но и для любой дифференцируемой функции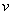 . Таким образом, результат применения правила дифференцирования сложной функции
. Таким образом, результат применения правила дифференцирования сложной функции 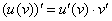 следующий:
следующий:
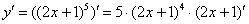
Снова подчеркиваю, что когда мы берем производную от внешней функции 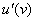 , внутренняя функция
, внутренняя функция 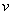 у нас не меняется:
у нас не меняется:
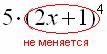
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:
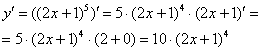
Готово.
Пример 4
Найти производную функции 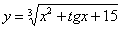
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени 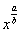 . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
. Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
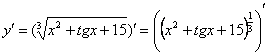
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции 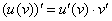 :
:

Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:

Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 5
Найти производную функции 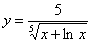
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного 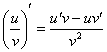 , но такое решение будет выглядеть
, но такое решение будет выглядеть как извращение необычно. Вот характерный пример:
Пример 6
Найти производную функции 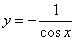
Здесь можно использовать правило дифференцирования частного 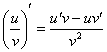 , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
, но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
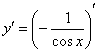
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
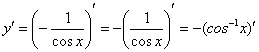
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило 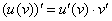 :
:
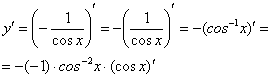
Находим производную внутренней функции, косинус сбрасываем обратно вниз:
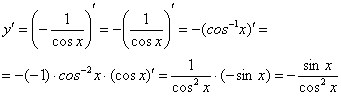
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила 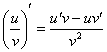 , ответы должны совпасть.
, ответы должны совпасть.
Пример 7
Найти производную функции 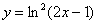
Это пример для самостоятельного решения (ответ в конце урока).
Пример 8
Найти производную функции 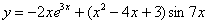
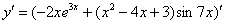
Сначала используем правило дифференцирования суммы 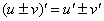 , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу
, заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу 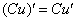 :
:
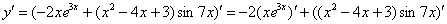
В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило 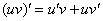 :
:
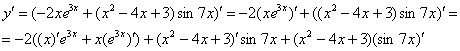
Замечаем, что под некоторыми штрихами у нас находятся сложные функции 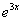 ,
, 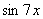 . Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
. Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу 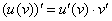 , получаем:
, получаем:
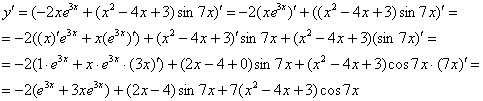
Готово.
! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.
Пример 9
Найти производную функции 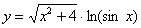
Это пример для самостоятельного решения (ответ в конце урока).
Ответы:
Пример 2: 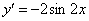
Пример 7: 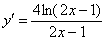
Пример 9: 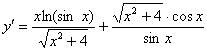
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|