Контакты

Случайная статья

Первообразная функции.. Геометрическая иллюстрация первообразной

Стр 1 из 2Следующая ⇒

Первообразная функции.

Определение 1. Пусть на некотором промежутке X задана функция 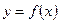. Функция 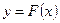, определённая на X, называется первообразной для 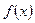на этом промежутке, если для всех 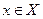верно равенство .

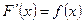Под промежутком X будем понимать отрезок, интервал, полуинтервал: , , , , , , , .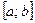

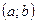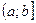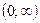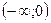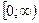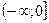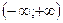Примеры:

1) ,

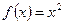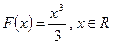
2) ,

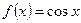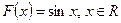
3) ,

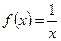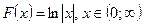
4) ,

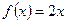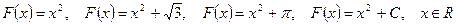
У всякой функции существует бесконечно много первообразных. Следующая теорема позволяет свести нахождение всех первообразных данной функции к отысканию одной из них.

Теорема.Есл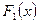и и 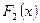– две первообразные от функции 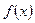на промежутке X, то

.

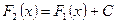Геометрическая иллюстрация первообразной

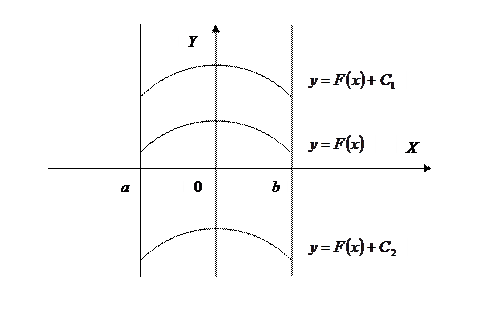
Графики всех первообразных получаются из графика одной первообразной параллельным переносом вдоль оси ординат.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.