Хелпикс

Главная

Контакты

Случайная статья



ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10. Краткие теоретические сведения



ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10

Тема: Комплексные числа в алгебраической форме: решение задач 

Краткие теоретические сведения

Алгебраическая форма - это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y), записывается в виде z = x + i y, где использован символ i , называемый мнимой единицей.

Сложение и вычитание комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 осуществляется по правилам сложения и вычитания двучленов (многочленов) x1 + i y1 и x2 + i y2 , т.е. в соответствии с формулами

z1 + z2 = x1 + i y1 + x2 + i y2 = x1 + x2 + i (y1 + y2),

z1 – z2 = x1 + i y1– (x2 + i y2) = x1– x2 + i (y1– y2).

Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид: i 2 = – 1 .

По этой причине

z1 z2 = (x1 + i y1) (x2 + i y2) = x1x2 + i x1 y2 + i y1x2 + i 2 y1 y2 =
= x1x2 + i x1y2 + i y1x2 – y1 y2 = x1x2 – y1 y2 + i (x1 y2 + i x2 y1) .

Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле

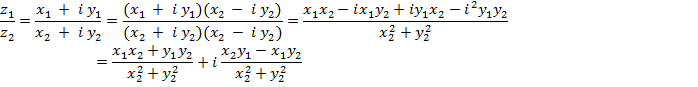
Пример 1. Сложить два комплексных числа ,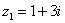

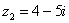
Решение: Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

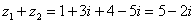
Пример 2. Найти произведение комплексных чисел ,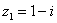

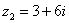
Решение: Получаем 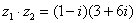 и раскрываем скобки по правилу умножения многочленов.

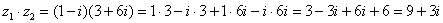
Пример 3. Даны комплексные числа 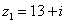, 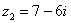. Найти частное .

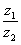Решение: Составим частное:

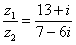
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Знаменатель нужно умножить на 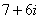, и, чтобы ничего не изменилось, домножить числитель на то же самое число :

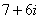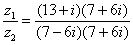
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем примере). А в знаменателе воспользоваться формулой 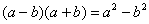(помним, что 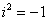и не путаемся в знаках!).

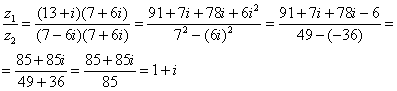
Содержание работы

Вариант 1.

Задание 1. Сложить два комплексных числа z1 = 3+7i, z2 = 5i – 4

Задание 2. Найти произведение комплексных чисел z1 = 10+2i, z2 = 5 – 3i

Задание 3.Даны комплексные числа z1 = 1+8i, z2 = 3i – 2. Найти частное .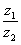

 

Вариант 2.

Задание 1. Сложить два комплексных числа z1 = 6+i, z2 = 2i – 10

Задание 2. Найти произведение комплексных чисел z1 = 1+12i, z2 = 3 – 3i

Задание 3.Даны комплексные числа z1 = 2+4i, z2 = 5i – 9. Найти частное .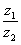

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.