Контакты

Случайная статья

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11. Краткие теоретические сведения. Действия с комплексными числами, заданные в тригонометрической форме

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11

Тема:Комплексные числа, тригонометрическая форма комплексного числа: решение задач

Краткие теоретические сведения

Любое отличное от нуля комплексное число z = x + i y может быть записано в виде

z = r (cos φ + i sin φ), (1)

где r и φ - модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .

Запись комплексного числа в форме (1) называют тригонометрической формой записи комплексного числа.

Действия с комплексными числами, заданные в тригонометрической форме

Модуль произведения комплексных чисел равен произведению модулей, а аргумент произведения равен сумме аргументов сомножителей.

Если 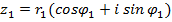, , 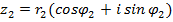то

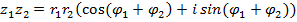
Для возведения комплексного числа в натуральную степень нужно возвести в эту степень его модуль, а аргумент умножить на показатель степени

Если 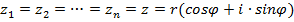, то

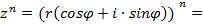
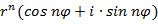
Модуль частного двух комплексных чисел 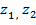равен частному модулей, а аргумент частного – разности аргументов.

Если 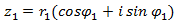, , 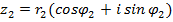то

))

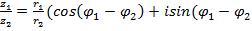Корень из комплексного числа z = r (cos φ + i sin φ), будет комплексное число вида

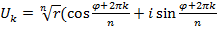), k=0,1,2,…n-1

Пример 1.Умножить числа 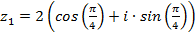и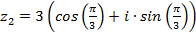

Решение: 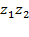= =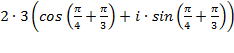6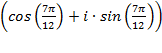

Пример 2.Возвести в степень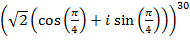

Решение: =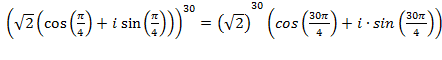

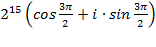
Пример 3. Даны комплексные числа ;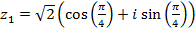

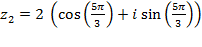
Найти частное .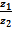

Решение: = =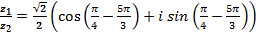

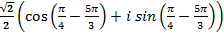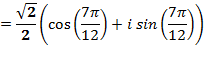
Пример 4. Найти все значения корня 3-ей степени из комплексного числа

.

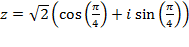Решение: 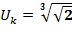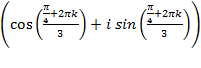, где k=0; 1; 2.

; ;

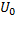
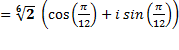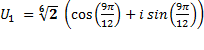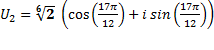
Содержание работы

Вариант 1.

Пример 1. Умножить числа 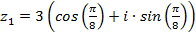и

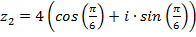
Пример 2. Возвести в степень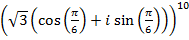

Пример 3. Даны комплексные числа 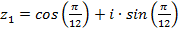и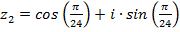

Найти частное .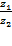

Пример 4. Найти все значения корня 3-ей степени из комплексного числа

.

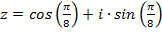Вариант 2.

Пример 1. Умножить числа 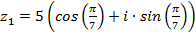и

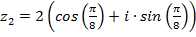
Пример 2. Возвести в степень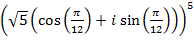

Пример 3. Даны комплексные числа 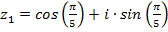и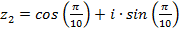

Найти частное .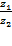

Пример 4. Найти все значения корня 3-ей степени из комплексного числа

;

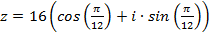© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.