Системы неравенств с одной переменной.

8-й кл. 13.04.

"Системы неравенств с одной переменной".

формировать умения решать системы линейных неравенств;

способствовать развитию элементов творческой, самостоятельной деятельности учащихся

1. Актуализация знаний.

1.Какие неравенства соответствуют промежуткам ( показать стрелочками )

x≤7 (3;+∞)

х>3 (-∞;7]

х<3 [-1;9)

-1≤х<9 (-∞;3)

2. Записать ответы

1. Какие из целых чисел принадлежат промежутку [0;4]?

2. Принадлежит ли промежутку (1,5; 2,4) число: 2;?

3. Какие из натуральных чисел принадлежат промежутку (-4;3]?

4. Используя координатную прямую найдите пересечение и

объединение промежутков (—3;+ 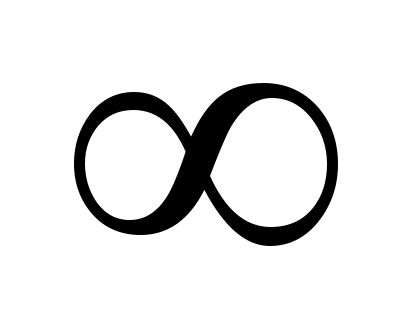) и |4;+ ).

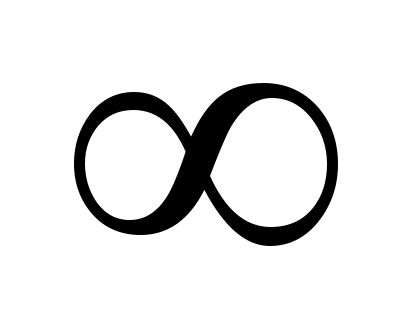2. Самостоятельная работа. Образец оформления:

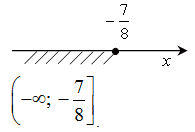а) 5(х – 1) + 7 < 1 – 3(х + 2);

5х – 5 + 7 < 1 – 3х – 6; 5х + 3х < 5 – 7 + 1 – 6; 8х < –7; -∞ +∞ х < –7 : 8; х <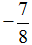

а)4 +12х > 7+13х ; б) 7-4х < 6х-23; в) 4(6+х) -(2-3х)> 1. г) 2(3+х) - (4-5х) ≤ 9.

Формирование умений и навыков. № 882 ( б, г) На всех координатных прямих отмечаем -∞ и +∞

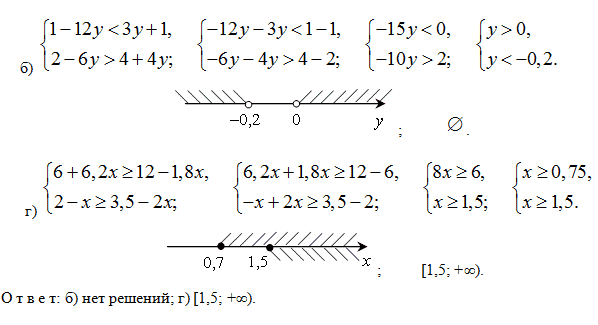
№ 883 ( б, г) Допустимы те значения переменной, при которых подкоренные выражения неотрицательны:

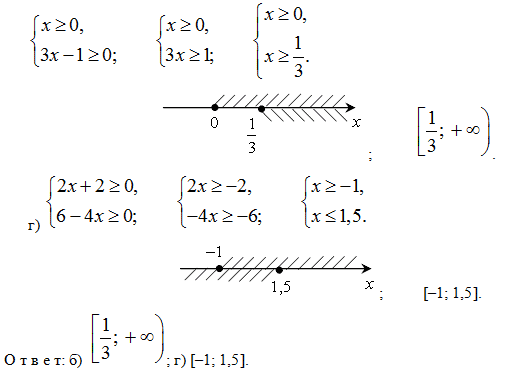
№ 884. б) В область определения функции 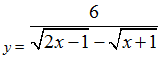входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.

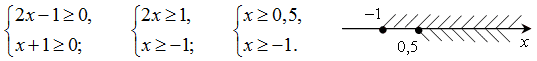
Знаменатель равен нулю, если:

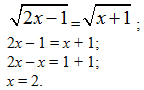
Значит, из области определения функции необходимо исключить х = 2.

3. № 886 (б, г)

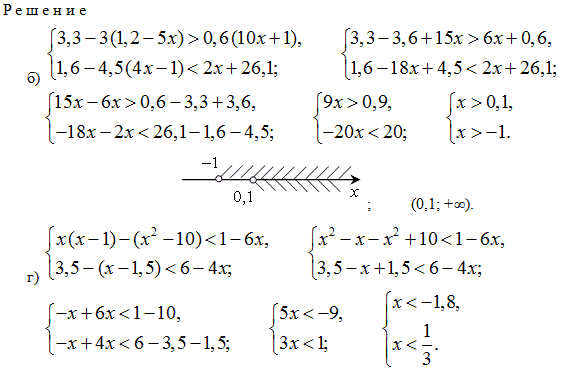
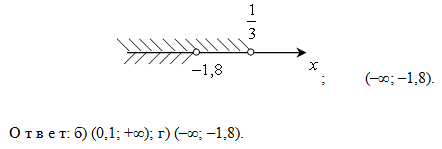
4. № 887 (б, г).

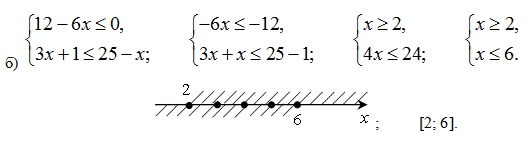
Целыми решениями являются: 2; 3; 4; 5; 6.

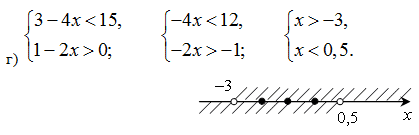
Целыми решениями являются: –2; –1; 0.

О т в е т: б) 2; 3; 4; 5; 6; г) –2; –1; 0.

Откройте учебник на стр.197 и решите пример 5( двойное неравенство )

Итоги урока

В о п р о с ы у ч а щ и м с я:

– Что называется решением системы неравенств?
– Что значит «решить систему неравенств»?
– Каков алгоритм решения системы неравенств?
– Сколько решений может иметь система неравенств?

Домашнее задание: Прочитать п.35 с.194,

Решить: № 877(а, в), № 879(б), № 881,