
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 1.
Рассмотрите примеры упрощения логических выражений, используйте законы логики, запишите в тетрадь:
Упрощение сложных высказываний - это замена их на равносильные, на основе законов алгебры высказываний, с целью получения высказываний более простой формы.
При упрощении сложных высказываний рекомендуется использовать основные законы преобразования логики и свойства констант.
Под упрощением формулы, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Пример 1.

(вынесем А за скобки и далее по закону исключения третьего)
Пример 2:
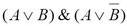
1 способ:
Применим закон дистрибутивности:

2 способ:
Перемножим скобки (как в алгебре чисел) и далее на основании закона дистрибутивности.
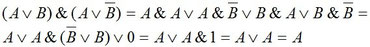
Пример 3 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:

Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
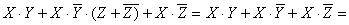
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
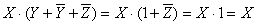
Таким образом,
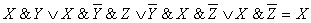
Пример 4 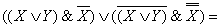
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
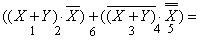
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
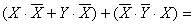
Воспользуемся операцией переменной с ее инверсией.
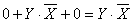
Таким образом,
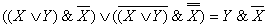
Пример 5 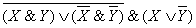
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
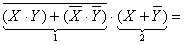
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.

Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
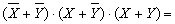
Применим закон склеивания 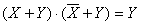
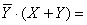
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
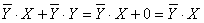
Таким образом,
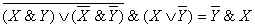
Пример 6Упростить логическое выражение 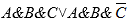
Последовательно применим дистрибутивный закон и закон исключенного третьего:
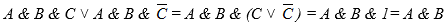
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|