
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Анализ контрольной работы. Системы линейных уравнений с двумя переменными
Анализ контрольной работы
Системы линейных уравнений с двумя переменными
1. Решить систему графическим способом:
а) 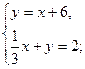
| х | -6 | |
| у | -2 |
| х | ||
| у |
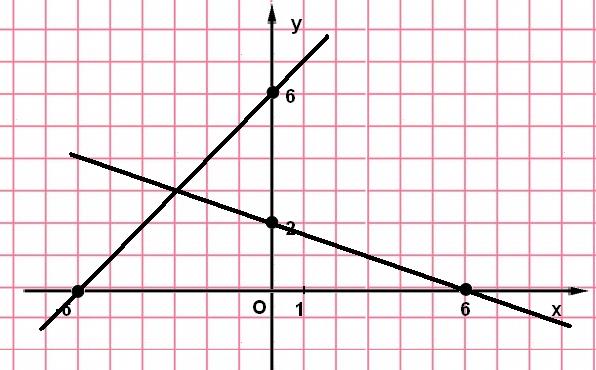
б) 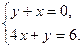
| х | ||
| у | -3 |
| х | ||
| у |

2. Решить систему уравнений способом подстановки:
а) 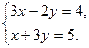
Выразим из второго уравнения х через у: х=5–3у.
Подставим в первое уравнение вместо х выражение 5–3у:
3(5–3у)–2у=4,
15–9у–2у=4,
–11у=–11,
у=1.
Подставляем в выражение х=5–3у вместо у число 1:
х=5–3∙1=2.
Ответ: (2; 1).
б) 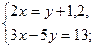
Из первого уравнения у=2х–1,2. Подставляем во второе уравнение вместо у выражение 2х–1,2:
3х–5(2х–1,2)=13,
3х–10х+6=13,
–7х=7,
х= –1.
у=2(–1)–1,2=–2–1,2=–3,2.
Ответ: (–1; -3,2).
в) 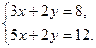
2у=8–3х.
5х+8–3х=12,
2х=4,
х=2.
2у=8–3∙2=2,
у=1.
Ответ: (2; 1).
3. Решить систему уравнений способом сложения:
а) 
Умножим обе части первого уравнения на 3, а обе части второго уравнения умножим на 2:
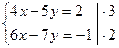
Получим: 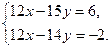
Вычтем почленно из первого уравнения второе:
12х–12х–15у–(–14у)=6–(–2).
Раскрываем скобки, складываем, получаем:
–у=8,
у= –8.
Подставляем в любое из уравнений вместо у число –8:
4х–5(–8)=2,
4х+40=2,
4х= –38,
х= –38:4= –9,5.
Ответ: (–9,5; -8).
б) 
Вычитаем почленно из второго уравнения первое:
8х–8х+20у–3у= –84–1,
17у= –85,
у= –5.
Подставляем вместо у число –5 в любое из уравнений:
8х+3(–5)=1,
8х–15=1,
8х=16,
х=2.
Ответ: (2; –5).
в) 
Складываем почленно первое и второе уравнения:
2х+4х–5у+5у=12+24,
6х=36, х=6.
2∙6–5у=12,
5у=0,
у=0.
Ответ: (6; 0).
4. Выясните, имеет ли решения система уравнений и сколько:
а) 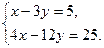

Домножим первое уравнение на 4:

Левые части обоих уравнений одинаковые, а правые не равны: 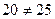 , значит прямые параллельны (не пересекаются), система решений не имеет.
, значит прямые параллельны (не пересекаются), система решений не имеет.
б) 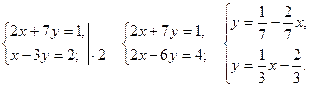
Коэффициенты при х в обоих уравнениях различны:  , значит, графики уравнений пересекаются в одной точке, система имеет единственное решение.
, значит, графики уравнений пересекаются в одной точке, система имеет единственное решение.
в) 
Оба уравнения совпадают, т.е. совпадают графики этих уравнений, система имеет бесконечное множество решений.
5.За 3 часа по течению и 4 часа против течения теплоход проходит 380 км. За 3 часа по течению и 1 час 30 мин против течения теплоход проходит 255 км. Найти собственную скорость теплохода и скорость течения реки.
Решение
Пусть х – собственная скорость теплохода, а у – скорость течения. Тогда скорость теплохода по течению будет равна х+у км/ч, против течения х–у км/ч. Составим и решим систему уравнений:
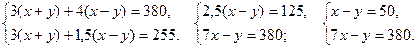
Складываем оба уравнения:
8х=420,
х=55 (км/ч).
у=х–50=55–50=5 (км/ч).
Ответ: 55 км/ч и 5 км/ч.
Домашнее задание

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|