
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры («Запишите в стандартном виде»)
Примеры («Запишите в стандартном виде»)
Представить числа а1, а2, а3, а4 в стандартном виде
а1 = 327 = 327,0 = 327 ∙ 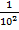 ∙102 = 3,27∙102 m = 2.
∙102 = 3,27∙102 m = 2.
а2 = 0,3 = 0,3 ∙ 10 ∙  = 3∙10-1 m = -1
= 3∙10-1 m = -1
а3 = 0,37 = 0,37 ∙ 10 ∙  = 3,7∙10-1 m = -1
= 3,7∙10-1 m = -1
а4 = 1827 = 1827,0 = 1827 ∙ 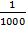 ∙ 1000 = 1,827∙103 m = 3
∙ 1000 = 1,827∙103 m = 3
Еще раз посмотрим на структуру числа, записанного в стандартном виде, на примере вышерассмотренных чисел:
а0∙ 10m,
где а0є [1; 10), m є Z
3,27 ∙ 102, где 3,27 – а0
1,827 ∙ 103, где 1,827 – а0
3 ∙ 10-1, где 3 – а0
Стандартный вид числа удобен для записи больших и малых чисел.
Расстояние до Солнца составляет 150 000 000 км. Записать это число в стандартном виде.
а = 150 000 000км
а = 150000000,0 = 1,5∙108 m = 8
Записать число b = 0,000038 в стандартном виде.
b = 0,000038 = 3,8∙10-5 m = -5
Скорость света равна V = 300 000 км/с. Записать это число в стандартном виде.
V = 300000,0 = 3∙105
Ответ: V = 3∙105m = 5
1 световой год равен 30 860 000 000 000км. Записать это число в стандартном виде.
1с.г. = 30 860 000 000 000 = 3,086∙1013км m = 13
Вычислить и представить в стандартном виде.
1) (0,2∙105) ∙ (1,4∙10-2) = 0,28∙103 = 2,8∙10-1∙103 = 2,8∙102 m = 2
2) (0,004)2 = (4,0∙10-3)2 = 16∙10-6 = 1,6∙10∙10-6 = 1,6∙10-5 m = -5
Пример («Сравните…»)
Сравните числа а и b
а = 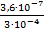 ; b = 0,001
; b = 0,001
а = 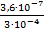 = 1,2∙10-7-(-4) = 1,2∙10-3 m = -3
= 1,2∙10-7-(-4) = 1,2∙10-3 m = -3
b = 0,001 = 1∙10-3 m = -3
Так как порядок двух чисел одинаковый, но 1,2 > 1, то а > b.
Ответ: а > b
Вывод
Итак, мы узнали, что такое стандартный вид положительного числа. Выяснили, каким образом получить стандартный вид положительного числа. Убедились на конкретных примерах, что стандартный вид положительного числа удобен для больших и малых чисел.
Практикум
Представьте в стандартном виде числа:
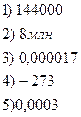
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|