
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Сокращение алгебраических дробей
Тема: Сокращение алгебраических дробей
-Для чего может пригодиться это умение?
-Что необходимо знать и уметь для того, чтобы сократить алгебраическую дробь?
(Таблицу умножения, формулы сокращённого умножения, правила выполнения действий со степенями, действий с одночленами и многочленами; алгоритм сокращения дробей; применять указанные знания на практике, раскладывать многочлен на множители разными способами…)
Алгоритм сокращения дроби:
1.Разложить на множители числитель и знаменатель дроби, если это необходимо.
2.Разделить числитель и знаменатель дроби на ненулевой многочлен.
3.Записать полученную дробь.

v Формулы сокращённого умножения (Слайд 3)
a2- b2= (a - b)(a + b)
a3- b3= (a - b)(a2 + ab + b2)
a3+ b3= (a + b)(a2- ab + b2)
a2 + 2ab + b2= (a + b)2
a2- 2ab + b2= (a - b)2
- При использовании формул квадрата суммы или квадрата разности учитывайте, что
(– а – b)2 = (а + b)2;
(b – а)2 = (а – b)2.
Это следует из того, что (– а)2 = а2.
v Фокусы с помощью формул сокращённого умножения (Слайд 4)
- А где ещё применяются формулы сокращенного умножения?
(При доказательстве некоторых утверждений и тождеств.
На формулах сокращенного умножения основаны некоторые математические фокусы и загадки, позволяющие производить вычисления в уме.)
«Отгадывание задуманного числа»
· Задумайте число (до 10);
· Умножьте его на себя;
· Прибавьте к результату задуманное число;
· К полученной сумме прибавьте 1;
-Скажите мне число, которое у вас получилось и я отгадаю, какое число вы задумали.
Решение:x² + x + 1 + x = x² + 2x + 1 = (x + 1)²
Например,5·5 + 5 + 1 + 5 = 36, тогда x = √36 – 1 = 6 – 1 = 5.
v «Верю- не верю»
| № | Утверждение | Свой вариант |
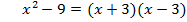
| ||
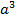 – 8 = (a + 2) ( – 8 = (a + 2) ( 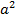 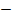 2a + 4) 2a + 4)
| ||
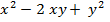 = = 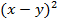
| ||
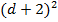 = = 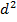 + 2d + 4 + 2d + 4
| ||
| 6pq – 18 p = 6p (q – 3) | ||
12 x + 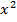 = x (12 + x) = x (12 + x)
| ||
| 27 + t3 = (3 + t)(9 – 6t + t2) |
v Путешествие в историю (Слайды)
Известный математик (1707 - 1783 гг.) родился в Швейцарии. В 1727 г. двадцатилетним юношей он был приглашен в Петербургскую Академию наук. Этот математик был соратником Ломоносова. В Петербурге он попадает в круг выдающихся ученых математиков, физиков, астрономов, получает широкую возможность для создания и издания своих трудов (их у него было более 800, и заняли они 72 тома). Среди его работ - первые учебники по решению уравнений. Старшеклассники учатся по учебникам, прообразы которых создал этот ученый. Его считают великим учителем математики. Последние в научном мире он работал слепым, но продолжал работать, диктовал труды своим ученикам. Однако в научном мире он больше известен как физик, который построил точную теорию движения луны с учетом притяжения не только Земли, но и Солнца.
Фамилию этого ученого вы узнаете, если правильно решите следующие пять заданий : разложите на множители способом группировки (Ученики решают эти задания, находят буквы в таблице результатов. Читают слово: Эйлер). < Слайд 12>
v Примеры:
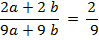
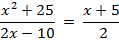
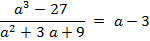
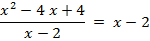
Самостоятельная работа № 1

Самостоятельная работа № 2

Самостоятельная работа № 3
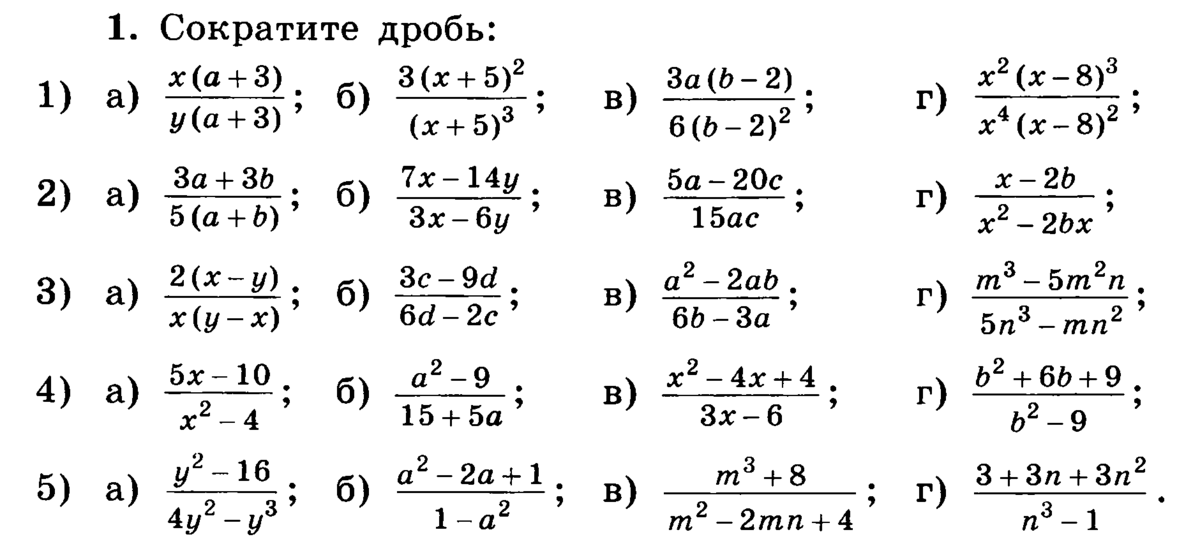
Самостоятельная работа № 4

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|