
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №9. вариант. вариант
Практическая работа №9
Тема: «Выполнение операций над множествами»
Цель: развитие практических навыков задания множеств, выполнения операций над множествами.
Время выполнения: 90 минут.
Ход работы:
Обязательное задание.
1. Найдите объединение, пересечение, разность множеств А и В, если:
а) А = ] 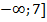 ; B=[1; +
; B=[1; + 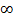 )
)
б) А =[3; 7] B=[0; 9] .
2. (Устно)Найдите дополнение в множестве всех треугольников к множеству:
а) всех равносторонних треугольников;
б) всех равнобедренных треугольников;
в) всех прямоугольных треугольников.
3. Пусть А = {2; 3; 4; 5; 7; 10}, В = {3; 5; 7; 9}, С ={4; 9; 11}. Найти множества:
а) А  (В
(В  С); е) А\В;
С); е) А\В;
б) (С 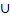 В)
В) 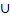 А; ж) А
А; ж) А 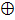 В;
В;
в) А 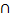 (В
(В 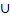 С); з) В
С); з) В 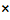 С.
С.
г) А 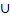 (В
(В 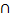 С);
С);
д) А 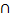 (В
(В 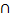 С);
С);
4.(Устно)Приведите примеры множеств, составленных из объектов следующих видов:
а) неодушевленных предметов;
б) животных;
в) растений;
г) геометрических фигур;
д) населенных пунктов;
е) водоемов;
ж) политических деятелей.
Индивидуальное задание.
1 вариант
1. Пусть А – множество корней уравнения 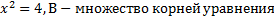
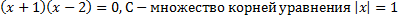 . Перечислите элементы множеств:
. Перечислите элементы множеств:
а) А 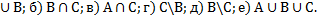
2. Перечислите элементы каждого из множеств:
а) А = {x : x 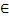 N , -2 ≤ x ≤ 5};
N , -2 ≤ x ≤ 5};
б) В = {х : x 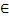 Z , | x | < 3};
Z , | x | < 3};
в) С = {х : x 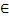 N , 2х2 + 5х –3 = 0}.
N , 2х2 + 5х –3 = 0}.
3.Даны множества: А= 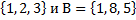 . Найдите А
. Найдите А 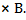
4.Даны два множества: А – множество стран и В – множество материков. Задайте соответствие между этими множествами с помощью стрелок. А= 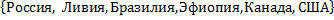 , В=
, В= 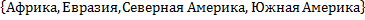 .
.
2 вариант
1. Пусть А – множество корней уравнения 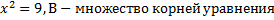
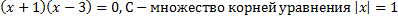 . Перечислите элементы множеств:
. Перечислите элементы множеств:
а) А 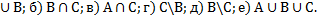
2. Перечислите элементы каждого из множеств:
а) А = {х : x 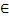 Z, | x | = 4};
Z, | x | = 4};
б) В = {х : x 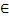 N , –2 < х ≤ 5};
N , –2 < х ≤ 5};
в) С = {х : x 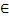 Q , x 2 + 3х + 4 = 0}.
Q , x 2 + 3х + 4 = 0}.
3.Даны множества: А= 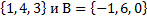 . Найдите А
. Найдите А 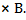
4.Даны два множества: А – множество месяцев года и В – множество времён года. Задайте соответствие между этими множествами с помощью стрелок.
3 вариант
1. Пусть А – множество корней уравнения 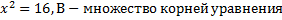
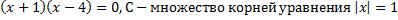 . Перечислите элементы множеств:
. Перечислите элементы множеств:
а) А 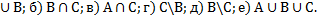
2. Перечислите элементы каждого из множеств:
а) А = {х: x 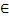 Z, –2 ≤ x ≤ 3};
Z, –2 ≤ x ≤ 3};
б) В = {х : x 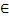 N , (5х + 6)(х – 4) = 0};
N , (5х + 6)(х – 4) = 0};
в) С = {х : x 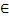 N , |x| = 7}.
N , |x| = 7}.
3.Даны множества: А= 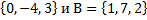 . Найдите А
. Найдите А 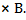
4.Даны два множества: А – множество стран и В – множество материков. Задайте соответствие между этими множествами с помощью стрелок. А= 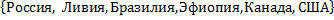 , В=
, В= 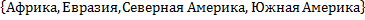 .
.
4 вариант
1. Пусть А – множество корней уравнения 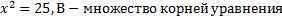
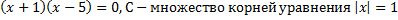 . Перечислите элементы множеств:
. Перечислите элементы множеств:
а) А 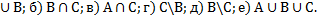
2. Перечислите элементы каждого из множеств:
а) А = {х : х 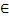 N, х ≤ 4};
N, х ≤ 4};
б) В = {х : х 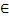 Z, (х + 1)(–х – 3) = 0};
Z, (х + 1)(–х – 3) = 0};
в) С = {х : х 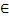 N, | х | = 5}.
N, | х | = 5}.
3.Даны множества: А= 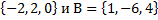 . Найдите А
. Найдите А 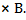
4. Даны два множества: А – множество месяцев года и В – множество времён года. Задайте соответствие между этими множествами с помощью стрелок.
Контрольные вопросы:
1. Назовите элементы, принадлежащие множеству:
а) студентов вашей группы;
б) предметов, изучаемых в I семестре вашей специальности;
в) всех частей света;
г) субъектов федерации, входящих в Российскую Федерацию.
2. Пусть А – множество многоугольников. Принадлежат ли этому множеству:
а) восьмиугольник;
б) параллелограмм;
в) отрезок;
г) параллелепипед;
д) круг;
е) полукруг?
3.Запишите перечислением элементов следующие множества:
а) А – множество нечетных чисел на отрезке [1; 15];
б) В – множество натуральных чисел, меньших 8;
в) С – множество натуральных чисел, больших 10, но меньших 12;
г) D – множество двузначных чисел, делящихся на 10;
д) Е – множество натуральных делителей числа 18;
е) F – множество чисел, модуль которых равен  .
.
4.На факультете филологии и журналистики учатся студенты, получающие стипендию, и студенты, не получающие стипендию. Пусть А – множество всех студентов факультета; В – множество студентов факультета, получающих стипендию.
Укажите, что собой представляет объединение, пересечение и разность множеств А и В.
Для отчёта представить:
1) Решение индивидуального задания.
2) Письменные ответы на контрольные вопросы.
Критерии оценки:
«5» - выполнено 90-100% всех заданий;
«4» - выполнено 70-90% всех заданий;
«3» - выполнено 50-70% всех заданий;
«2» - выполнено менее 50% всех заданий.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|