
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Домашнее задание .Разберите задачи урока, почитайте п.77,78, 71.
16.04. Урок геометрии в 9 классе.
Тема: «Вписанные и описанные окружности».
Цель и задачи урока:
- повторить и обобщить основные сведения о вписанных и описанных окружностях.
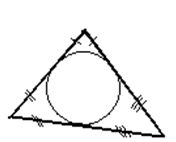
Повторение.
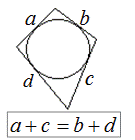
| 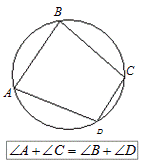
| 
|
| 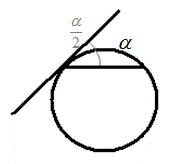
| 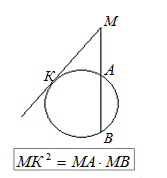
|

| 
| 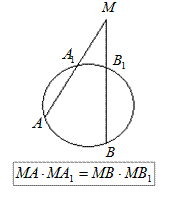
|
Решение задач по готовому чертежу.
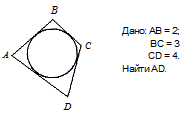
|
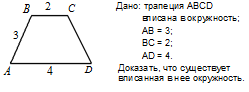
| 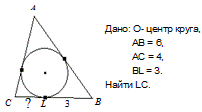
|
1)Так ка АВ+СД=ВС+АД, тоАД=АВ+СД-ВС=2+4-3=3
2)Здесь дана равнобедренная трапеция. Но мы видим, чтоАВ+СД=ВС+АД значит можно вписать окружность.
3)СL=1(смотри свойство на стр. 165)
 Решение:
Решение:
AE∙BE=CE∙DE  DE=
DE= 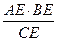 =
=  =20
=20
Ответ: DE=20
4)
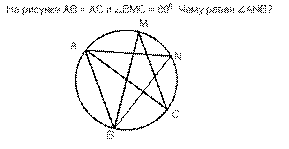 Решение:
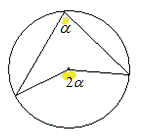
Решение:  ВАС=
ВАС=  ВМС=800 т.к они опираются на одну дугу ВС. ΔВАС-равнобедренный, т.к. АВ=АС
ВМС=800 т.к они опираются на одну дугу ВС. ΔВАС-равнобедренный, т.к. АВ=АС 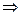
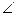 АВС=
АВС= 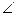 АСВ=
АСВ= 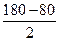 =500.
=500.
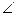 АNB=
АNB= 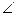 АСВ=500.
АСВ=500.
Ответ: 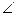 АNB=500.
АNB=500.
5) Из одной точки проведены две касательные к окружности. Точки касания делят окружность на две дуги, относящиеся друг к другу как 1:9. Найдите угол между касательными.
 В
В
 А
А 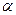
С

Решение:
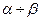 =1:9. Пусть
=1:9. Пусть 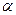 =Х0, тогда
=Х0, тогда  =9Х0.
=9Х0.
Получим уравнение: х+9х=360
10х=360
х=360.
Следовательно, 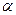 =360,
=360,
 =9∙360=3240.
=9∙360=3240.
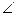 АBС=
АBС= 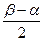 =
=  =1440.
=1440.
Ответ: 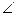 АBС=1440.
АBС=1440.
6)
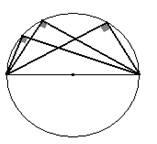
Докажите, что диаметр окружности, проведённый через середину хорды
(не являющейся диаметром), перпендикулярен этой хорде.
В



 С
С
 E
E
 D
D
O
Доказательство. OE – медиана треугольника COD.
Так как OC = OD, треугольник COD равнобедренный. Следовательно, OE является высотой треугольника COD. Поэтому AB  CD.
CD.
Домашнее задание .Разберите задачи урока, почитайте п.77,78, 71.
Выполнить ГИА Заканчивайте решать блок 5.1-5.80 ( Вы уже решаете
эти задания 3 неделю). Прошу начать сдавать эти задания. Можно по частям.
С уважением, Светлана Владимировна.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|