
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Казахская головная архитектурно-строительная академия
Казахская головная архитектурно-строительная академия
Активный раздаточный материал
Математика 1 ФОЕНП
Кредит 1-ый семестр
Лекция № 9. Числовая последовательность и ее предел. Предел функции. 2011-2012 уч.г.
Ассоц. профессор Сыдыкова Дамелькан Какеовна
Определение. Числовой последовательностью называется действительная функция натурального аргумента, т. е. функция, у которой 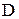 =N и ЕÌR.
=N и ЕÌR.
Она обозначается символом  , где
, где 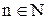 , или короче,
, или короче, 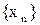 . Число
. Число 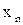 , зависящее от n, называется n –ым членом последовательности. Расставив значения последовательности по порядку номеров, получаем, что последовательность можно отождествить со счётным набором действительных чисел, т. е.
, зависящее от n, называется n –ым членом последовательности. Расставив значения последовательности по порядку номеров, получаем, что последовательность можно отождествить со счётным набором действительных чисел, т. е.
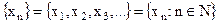 .
.
Примеры:а) Последовательность 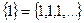 являет ся постоянной и состоит из равных чисел (единиц):
являет ся постоянной и состоит из равных чисел (единиц): 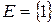 ; б)
; б) 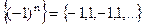 . Для неё
. Для неё 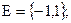 в)
в) 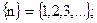 г)
г) 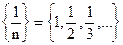 .
.
Определение. Число а, называется пределом последовательности 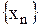 , если для любого числа
, если для любого числа 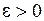 найдётся число
найдётся число 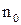 , что все числа
, что все числа  , у которых
, у которых  , удовлетворяют неравенству
, удовлетворяют неравенству 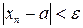 .
.
Соответствующее обозначение 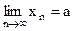 .
.
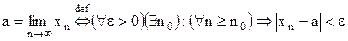 .
.
Геометрически определение предела последовательности означает следующее: для сколь угодно малой  -окрестности числа анайдется такой номер N, что все члены последовательности с большими, чем N, номерами попадают в эту окрестность, вне окрестности оказывается лишь конечное число начальных членов последовательности (рис. 9.2). Это все или некоторые из членов
-окрестности числа анайдется такой номер N, что все члены последовательности с большими, чем N, номерами попадают в эту окрестность, вне окрестности оказывается лишь конечное число начальных членов последовательности (рис. 9.2). Это все или некоторые из членов  .
.
 |
x1 x2 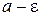 xN+1 a xN+2
xN+1 a xN+2 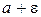 xN x3
xN x3
Определение. Число А называется пределом функции  при
при 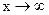 , если
, если 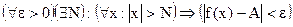 . (Обозначается
. (Обозначается 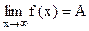 ).
).
Первый замечательный предел 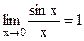 .
.
Пример. 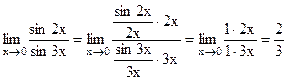 .
.
Второй замечательный предел
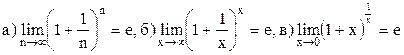 .
.
Здесь е»2,718282… – иррациональное число.
Пример. Вычислим предел
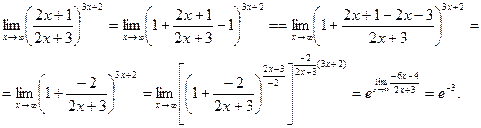
Задание на СРС
1. Теоремы о бесконечно малых и о пределах функций. (конспект, по графику) [1,3,4].
2. Решение задач по теме [ 2. ИДЗ-5.1-5.2 стр. 166 ].
Задание на СРСП
1. Вычисление пределов функций.
Контрольные вопросы:
1. Определение числовой последовательности и ее предела, функции.
2. Какие последовательности называются ограниченными, монотонными?
3. Действия над последовательностями и функциями, виды неопределенностей.
1. Множество, где функция 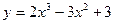 убывает, есть А.
убывает, есть А. 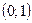 ; В.
; В. 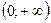 ; С.
; С. 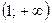 ; Д.
; Д. 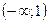
2. Вычислить предел 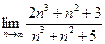 А.
А. 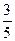 ; В. 2; С. 1; Д.
; В. 2; С. 1; Д. 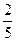
3. Вычислить предел 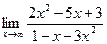 А.
А. 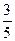 ; В. 1; С.
; В. 1; С. 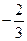 ; Д. 2
; Д. 2
4. Вычислить предел последовательности 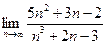 А. 3; В.
А. 3; В. 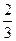 ; С. 5; Д. 0
; С. 5; Д. 0
5. Найти предел функции 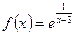 при x→3 А. 1; В. 0; С.
при x→3 А. 1; В. 0; С. 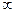 ; Д. 2
; Д. 2
6. Найти точку разрыва функции 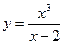 А. -2; В. 2; С. 0; Д. 1
А. -2; В. 2; С. 0; Д. 1
7. Найти область определения функции 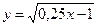 А.
А.  ; В. (-4; 4); С.
; В. (-4; 4); С. 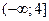 ; Д. (
; Д. ( 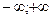 )
)
8. . Вычислить предел 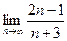 А. 1; В. 0; С. 2; Д.
А. 1; В. 0; С. 2; Д. 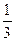
9. Вычислить предел функции 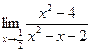 А.
А. 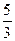 ; В.
; В. 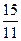 ; С. 3; Д.
; С. 3; Д. 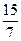
10. Вычислить предел  А.
А. 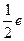 ; В.
; В. 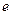 ; С.
; С. 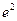 ; Д.
; Д. 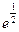
11. Вычислить предел 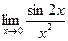 А. 2; В. 1; С.
А. 2; В. 1; С. 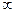 ; Д. 0
; Д. 0
12 Вычислить предел 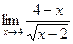 А. 2; В. -2; С. 4; Д. 0
А. 2; В. -2; С. 4; Д. 0
Список литературы:
Основная:
- Бугров Я.С., Никольский С. М., Элементы линейной алгебры и аналитической геометрии. 1999
- А.Т. Рябушко Сборник индивидуальных заданий по высшей математике часть 1.,2002г.
3. К. Кабдыкаир. Курс математики. Алматы, 2005.
Дополнительная:
4. В.Е. Шнейдер и д.р. Краткий курс высшей математики. 2001
5. Д.В. Клетеник Сборник задач по аналитической геометрии. 2000
6. Д.К.Сыдыкова. Математика-1. Методическое руководство к выполнению заданий для СРС, Алматы, 2008
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|