Урок: Определение параллельности прямой и плоскости. Теорема о признаке параллельности прямой и плоскости,

Урок: Определение параллельности прямой и плоскости. Теорема о признаке параллельности прямой и плоскости,

ЦЕЛЬ УРОКА: 1ввести понятие прямой, параллельной плоскости

2 при доказательстве теоремы развивать у обучающихся логическое мышление.

Ход урока

1. повторить определение параллельных, скрещивающихся прямых

2. теорему о единственности прямой, параллельной данной, проходящей через данную точку

3. повторить о двух параллельных прямых

4. дать определение параллельных прямой и плоскости

5. доказать теорему о параллельности прямой и плоскости

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

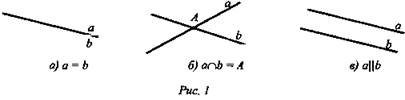
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Проиллюстрировать данные определения наглядно нам поможет куб.

Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.

Определение.Прямая и плоскость называются параллельными, если они не имеют общих точек.

Обозначение: a||α.

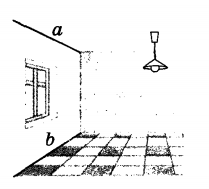
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

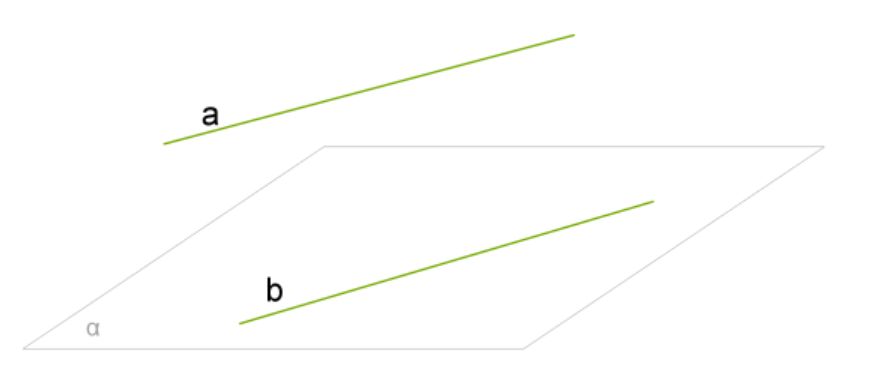
Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.

Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.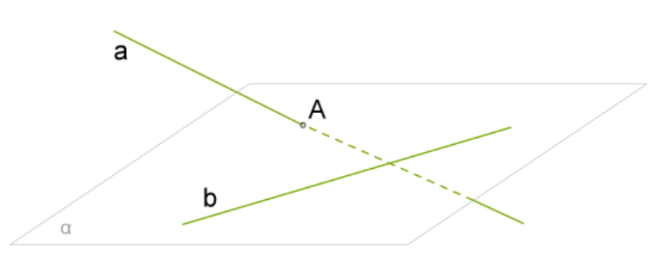

Существует еще два утверждения, которые используются при решении задач:

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

Закрепление материала.Задача:

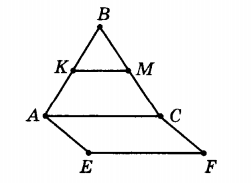
Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Найти: EF

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Ответ: EF=10

Дом. задание выучить определение, записать конспект урока.