
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формулы половинного аргумента.
Формулы половинного аргумента.
Сегодня мы узнаем формулы, позволяющие нам по известным значениям 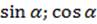 ;
; 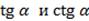 находить
находить 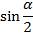 ;
; 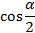 ;
; 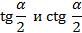 .
.
Их называют формулы половинного аргумента.
Повторим формулу косинуса двойного аргумента 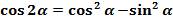 .
.
А если учесть, что 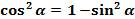 и
и 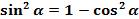 , то получим ещё две формулы, которые нам сегодня понадобятся:
, то получим ещё две формулы, которые нам сегодня понадобятся:
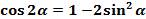 и
и 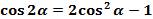
Пример.
а) Найти 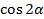 , если
, если 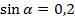 .
.
Вычислим 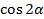 по формуле
по формуле 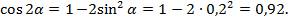
б) Найти 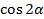 , если
, если 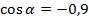 .
.
Вычислим 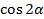 по формуле
по формуле 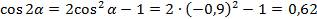 .
.
Запишем формулу косинуса двойного аргумента в виде 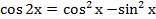 и заменим х на
и заменим х на  . Тогда получим:
. Тогда получим: 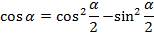 , учтём, что
, учтём, что
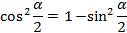 , получаем
, получаем
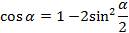
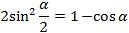
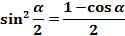 (1)формула синуса половинного аргумента.
(1)формула синуса половинного аргумента.
Запишем формулу косинуса двойного угла, где 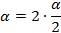 в виде
в виде
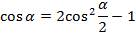
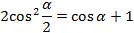
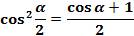 (2)формула косинуса половинного угла.
(2)формула косинуса половинного угла.
По формулам (1) и (2) можно найти 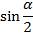 или
или 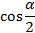 , если известны значения
, если известны значения 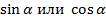 и положение угла
и положение угла 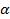 , т.е. в какой координатной четверти он находится, чтобы определить знак выражения
, т.е. в какой координатной четверти он находится, чтобы определить знак выражения 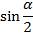 или
или 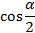 .
.
Эти формулы ещё имеют название «формулы понижения степени», так как в левой части находится вторая степень синуса и косинуса, а в правой – первая, т.е. степень понизилась. Но будьте внимательны: степень понижается, а аргумент удваивается.
Например, 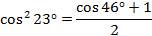 .
.
Пример.Известно, что 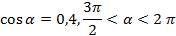 . Найдите
. Найдите 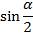 ;
; 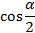 ;
; 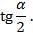
1) 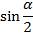 найдём по формуле:
найдём по формуле: 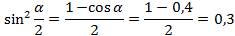 ;
; 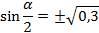 .
.
По условию 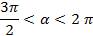 . Разделив обе части неравенства на 2, получаем
. Разделив обе части неравенства на 2, получаем 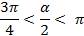 , значит угол
, значит угол  во второй четверти, здесь синус положительный.
во второй четверти, здесь синус положительный. 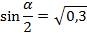 .
.
2) 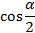 ; найдём по формуле
; найдём по формуле 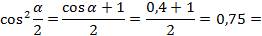 ,
, 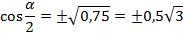
Мы уже выяснили, что угол  во второй четверти, косинус отрицательный.
во второй четверти, косинус отрицательный. 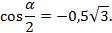
3) Так как тангенс это отношение синуса на косинус, то 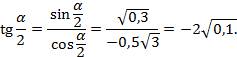
Выведем формулу для тангенса половинного аргумента. Для этого разделим левую часть формулы (1) на левую часть формулы (2) и правую часть формулы (1) на правую часть формулы (2).
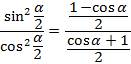 сократим на 2 , и учитывая, что
сократим на 2 , и учитывая, что 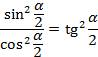 , получим:
, получим:
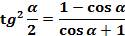 формула тангенса половинного аргумента (3).
формула тангенса половинного аргумента (3).
Так как котангенс это число, взаимообратное тангенсу, то 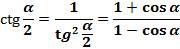
Пример. Найти 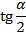 и
и 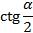 , если известно, что
, если известно, что 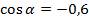 и
и 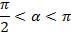 .
.
По формуле (3) находим 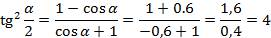 , а
, а 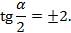 Найдём положение угла
Найдём положение угла 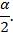
По условию 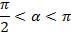 ,( разделим на 2)
,( разделим на 2)
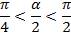 , угол
, угол  в первой четверти, тангенс положительный,
в первой четверти, тангенс положительный, 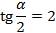 , а
, а 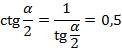 .
.
Выведем формулу, по которой можно найти 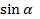 через
через 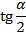 .
.
Для этого используем формулу синуса двойного угла 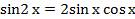 , заменив в ней х на
, заменив в ней х на  . Получаем
. Получаем 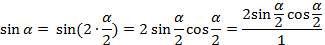 , учтём, что
, учтём, что 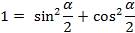 , то
, то
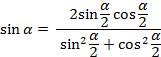 , разделим числитель и знаменатель на
, разделим числитель и знаменатель на 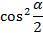 , получаем:
, получаем:
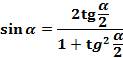 (4)
(4)
Выведем формулу для 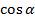 через
через 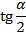 . Применим формулу косинуса двойного угла, где
. Применим формулу косинуса двойного угла, где  ,
, 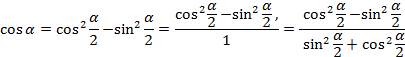 , разделим числитель и знаменатель на
, разделим числитель и знаменатель на 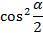 , получаем:
, получаем:
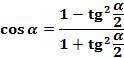 (5)
(5)
Пример. Найти 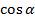 , если
, если 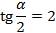 .
.
По формуле (5) 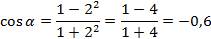 .
.
Если в формуле тангенса двойного угла 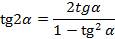 представить
представить 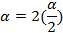 , то получим ещё одну формулу, по которой тангенс угла
, то получим ещё одну формулу, по которой тангенс угла 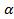 можно найти через тангенс угла
можно найти через тангенс угла  : tg
: tg 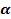 =
= 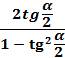
С помощью доказанных формул можно не только вычислять значения выражений, но и упрощать выражения, доказывать тождества и решать тригонометрических уравнений.
Пример. Доказать тождество 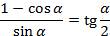 .
.
Представим 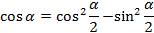 , а
, а 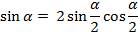 , преобразуем левую часть тождества
, преобразуем левую часть тождества
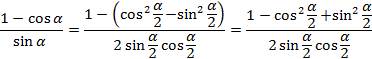 , но
, но 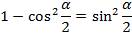 , то
, то
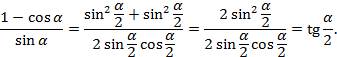
Левая часть равна правой части, тождество доказано.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|