Всероссийская олимпиада школьников по математике

2020 год

Всероссийская олимпиада школьников по математике

Муниципальный этап

10 класс

Решения

1. Преобразуем уравнение к виду (х² + 2х)² – 2021 (х² + 2х) + 2020 = 0. Введем новую переменную, обозначив t = (х² + 2х).

Получим уравнение t² – 2021t + 2020 = 0, корни которого t₁ = 1, и t₂ = 2020. Тогда х² + 2х =1 или х² + 2х = 2020. Откуда имеем х₁ = –1 + 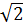, х₂ = –1 – ,

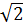х₃ = – 1 + 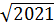, х₄ = – 1 – 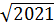. Их произведение равно 2020.

Ответ: произведение всех корней равно 2020.

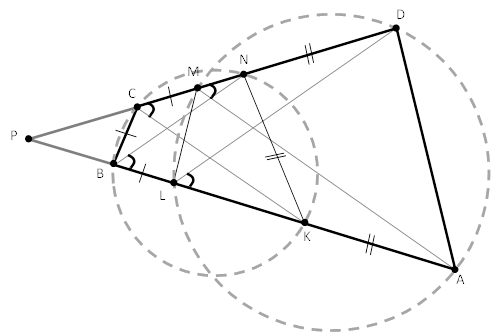
2. а) В случае АВ II CD имеем ВС = KN. Поэтому АК=BL=DN. Значит, четырехугольник LMDA получается из BCNK путем параллельного переноса на вектор .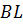

б) Пусть теперь АВ и СD не параллельны. Обозначим через Р точку пересечения прямых АВ и СD. Так как четырехугольник ВСNK вписан, то

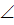NKL + 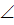ВCN = 180°. Также сумма углов РСВ и BCN равна 180°. Следовательно, 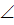NKL = 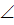РСВ. Тогда, треугольники PBC и PNK подобны. Отсюда: 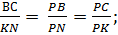получим ВС· PN = PB∙ KN, а отсюда и из условия, что ВС = КL имеем 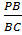= 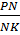. Но по условию задачи ВС = KL, а NK = ND, следовательно, имеет место равенство: 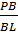= = 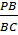= 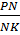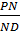. Значит, BN II LD.

Аналогично, доказываем, что СК II МА. Из подобия треугольников имеем равенство 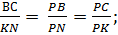отсюда получим РС∙ KN = BC∙ PK, отсюда имеем 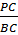= 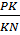. Из условия задачи имеем: ВС = СМ, KN = KA. Следовательно, имеет место равенство: 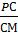= = 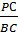= 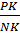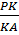. Значит, СК II MA.

Отсюда получаем Ð ALD = Ð KBN и Ð KCN = ÐAMD.

Так как четырехугольник BCNK можно вписать в окружность, то Ð KBN и Ð KCN равны, как вписанные, опирающиеся на одну и ту же дугу. Тогда, 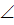ALD = 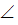KCN . Поэтому и 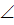ALD = 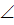AMD, то есть ADML также можно вписать в окружность.

3. Пусть доля учеников, сдававших обществознание и английский равна х, обществознание и немецкий – у, английский и немецкий – z все предметы – t. Тогда из условия задачи следует, что

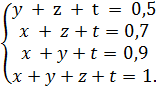
Решаем данную систему, получаем t =0,1.

Ответ: 10%

4. Координаты вершины параболы х_{0 =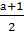} , у_{0 =}4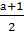₍ )² – 4 (а + 1) 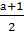+ а = -а² –а -1 = - (а + )² - . Так как у₀ < 0 при любых значениях а, то во второй координатной четверти вершина параболы находиться не может.

Ответ: нет, не может.

5. Пусть М – наибольшее из всех чисел, а перед ним стоят числа а и в. Тогда а + в = М², а £ М, в £ М, откуда М² £ 2М и М £ 2 (учитываем, что М > 0).

Пусть m – наименьшее из всех чисел, а перед ним стоят числа с и d. Тогда с + d = m² , c ≥ m, d ≥ m. Откуда m² ≥ 2m и m ≥ 2 (поскольку m > 0). Итак, наибольшее число не больше 2, а наименьшее – не меньше 2. Значит, все числа равны 2.

С другой стороны для 100 двоек выполняется условие задачи.

Ответ: сто двоек.